Guidobaldo structured his treatise on mechanics according to his goal to apply the ancient model of a deductive theory. The treatise starts with definitions (definitiones), axioms (communes notiones) and postulates (suppositiones). Following this short introductory part, the treatise continues with propositions (propositiones) together with their proofs. Some of the propositions are additionally designated as problems (problemata). This basic structure is occasionally complemented by auxiliary propositions (lemmata) preceding the propositions of a chapter and by corollaries (corollaria) adding one or more immediate consequences to a proposition.
While these formal distinctions which structure a theory were commonly accepted as a conceptual scheme inherited from the ancient model, this was not equally the case with regard to their meaning and their attributions to specific statements. In particular, the assignment of the three categories of preconditions to specific classes of assumptions, and especially whether a statement has to be qualified as an axiom or a postulate, varies from author to author. This is even more so for the subject of the propositions, the level of generality they represent and their grouping into content areas.
It has been mentioned already that Guidobaldo, according to Heron's analysis of machines1, formulated and grouped his propositions into certain elements and their classification into so-called simple machines. Heron's sophisticated analysis, however, was unknown to Guidobaldo and his contemporaries except for the fragmentary quotations provided by Pappus and made known to them through Commandino's translation2. Guidobaldo and his contemporaries had to reinvent the details of the propositions and their proofs. Thus the recourse to Heron's analysis of mechanical technology was not simply a revival of his work, but moreover an incentive for innovation and controversial discourse.
The order in which Pappus, and Commandino after him, arranged the simple machines differs from the one in Herons Mechanics.3 The five simple machines listed in Commandino's translation4 of Pappus' Mathematicae collectiones5 are:
wedge (cuneus)
lever (vectis)
screw (cochlea)
pulley (polyspaston)
axle (axe)
Guidobaldo reordered these five machines and complemented them with the balance as a sixth. Accordingly, his chapters are titled:
On the balance (De Libra)
On the lever (De Vecte)
On the pulley (De Trochlea)
On the axle in a wheel (De Axe in peritrochio)
On the wedge (De Cuneo)
On the screw (De Cochlea)
3.1 The Definitiones
Guidobaldo gives a definition for only one concept, the definition of the center of gravity.6 Literally following Commadino in his work on the center of gravity7 he gives two different definitions of the concept. Both Commandino and Guidobaldo define the center of gravity as a point of indifferent equilibrium. They correctly attribute this definition to Pappus8, who himself obviously took this definition from the Mechanics of Heron9 although not literally as a quotation.
The second definition given by Commandino and Guidobaldo is also taken from the Mechanics of Heron10, who attributed it to Archimedes, probably referring to one of his lost works.11 According to this second definition the center of gravity of a body is a point through which each cut divides the body into two parts of equal weight. This definition, attributed by Heron to Posidonius12, is obviously fallacious since it does not take into account the positions of the centers of gravity of the two parts. Guidobaldo adopts the two definitions from Commandino without comment.
3.2 The Communes notiones
In the further presuppositions13 of his treatise Guidobaldo followed neither Commandino nor Archimedes, although his own theory of equilibrium is based largely on Archimedes' treatise On the equilibrium of planes. Instead of using the postulates of Archimedes, which themselves are inspired by the axioms (common notions) in Euclid's Elements, Guidobaldo uses the first three axioms (common notions) of Euclid14 literally only replacing the term equal things by the term things of equal weight.
3.3 The Suppositiones
Guidobaldo adds three postulates (suppositiones) which essentially make assumptions about the center of gravity explicit. He assumes that the center of gravity of a body is unique and invariable. He further assumes that a body descends towards the center of the world according to his center of gravity.
3.4 The Chapter De Libra
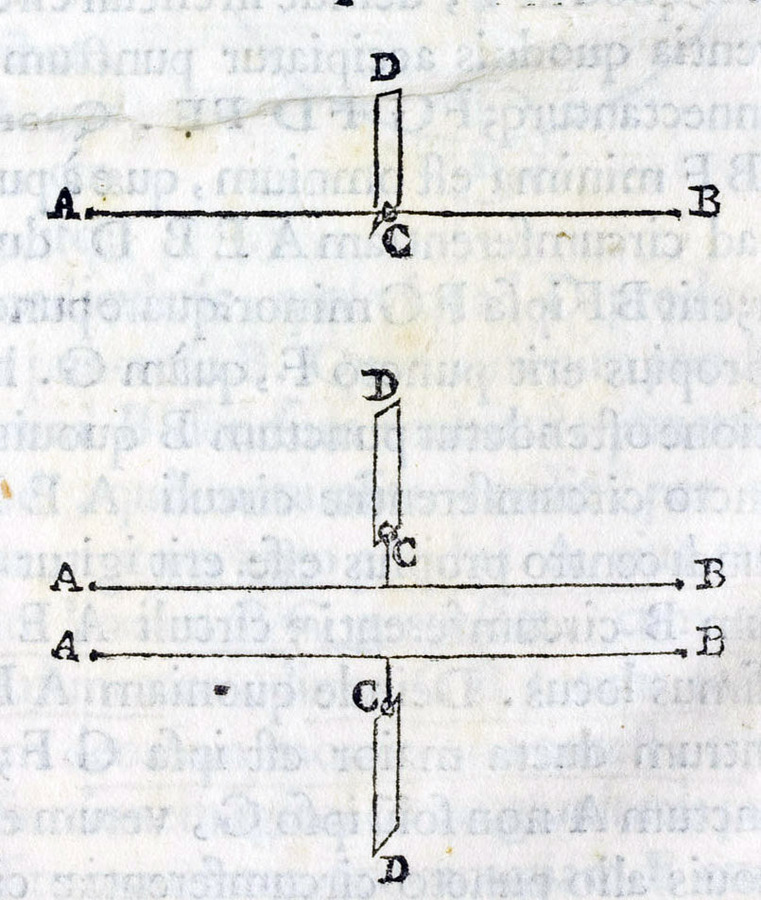
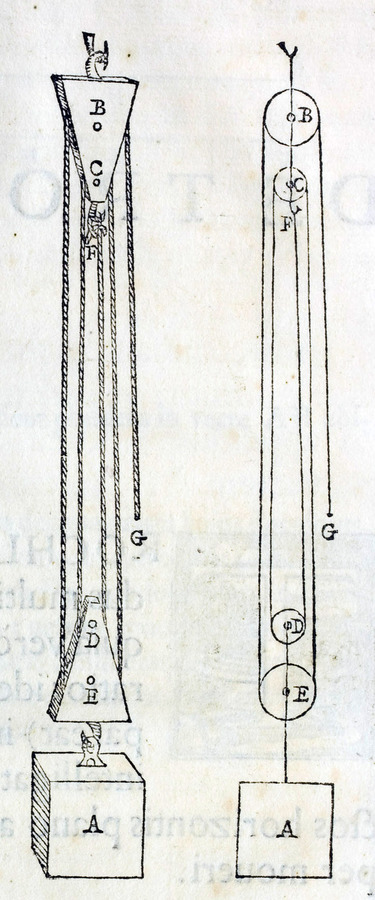
Fig. 3.1: The balance (libra) supported at, from above, and from below its center of gravity
The chapter on the balance15 begins with some explanations of terms related to this instrument, terms such as the support (trutina), the center of the balance (centrum librae) around which the balance turns, or the arms of the beam (librae brachia).
These explanations are followed by a geometrical lemma concerning the distances of different points on the circumference of a circle to a point outside the circle. From the context it becomes clear that the circle represents the end points of the beam of a balance turning around its center while the external point represents the center of the world.
The lemma thus indicates a major concern of Guidobaldo and his contemporaries: If heavy bodies tend to descend to the center of the world their lines of descent cannot be parallel. In modern terms, gravitation is truly a radial field around the center of the earth rather than a homogeneous one. While the lemma seems to play only a minor role, if any, in Guidobaldo's treatise it is nevertheless closely linked to Guidobaldo's extensive discussion against the arguments of his contemporaries, which he deems fallacious and criticizes in the sequel to his fourth proposition.
The lemma is followed by three propositions representing facts concerning the equilibrium of a balance which were well known from antiquity. In particular, the second and the third proposition deal with balances supported above or below their centers of gravity. They state that the equilibrium in these cases is not stable. This is essentially what has already been proven, although in another way, by the second problem of the Aristotelian Problemata mechanica.16
The following fourth proposition expresses a further major concern of Guidobaldo. He proves that the equilibrium of a balance is stable in every position if it is supported at its center of gravity. From a modern point of view this claim is a simple consequence of the definition of the center of gravity and this is also the gist of Guidobaldo's reasoning. Nevertheless, some medieval and early modern scholars such as Jordanus, Tartaglia and Cardano17 argued to the contrary. In reaction to their work, Guidobaldo complemented his fourth proposition with several pages of arguments that attempt to make evident that their alleged proofs were erroneous. He goes into great detail, attempting to show that even when their own conceptual means are applied – including the assumption that the directions in which the weights at the ends of the balance tend to descend are not parallel – it follows what he himself maintains, that is, that a balance is stable in every position if it is supported at its center of gravity.
The remaining propositions five to seven deal with what is now termed the law of the lever. This law provides the theoretical background for another type of balance, that is, the Roman steelyard (statera), a balance with unequal arms and a moving weight. Guidobaldo faced the conceptual difficulty of expressing the difference between the actual weight of a body and its varying effect if it is attached to different points on the beam of a balance.
This problem is an issue that was raised already in antiquity. It was transmitted to the Arabic culture and from there to scholars of the medieval Latin tradition. Jordanus made it well known through his work. He introduced the technical term “positional gravity” (gravitas secundum situm)18 for the effect of a weight positioned at some place on the beam of a balance.
It was Tartaglia who not only made Jordanus known in the Renaissance by editing his work19 but who also EOAemphasized the distinction of the actual weight and its effect when attached to the beam of a balance. For the effect of such a weight he gives an explicit definition, designating this effect as positional heaviness (grave secondo el luoco).20
Guidobaldo deals with the problem in an ambiguous way by using the term pondus for the actual weight of a body and the term with the same root ponderare for the varying effect when the body is attached to different places on the beam of a balance.
His fifth proposition concerns two weights hanging down from different places on the beam.
Two weights (pondera) attached to a balance. If the balance were divided in between so that the parts of the weight (partes ponderibus) correspond inversely, then they will weigh (ponderabunt) at the points they are attached as much as if each were suspended from the dividing point.21
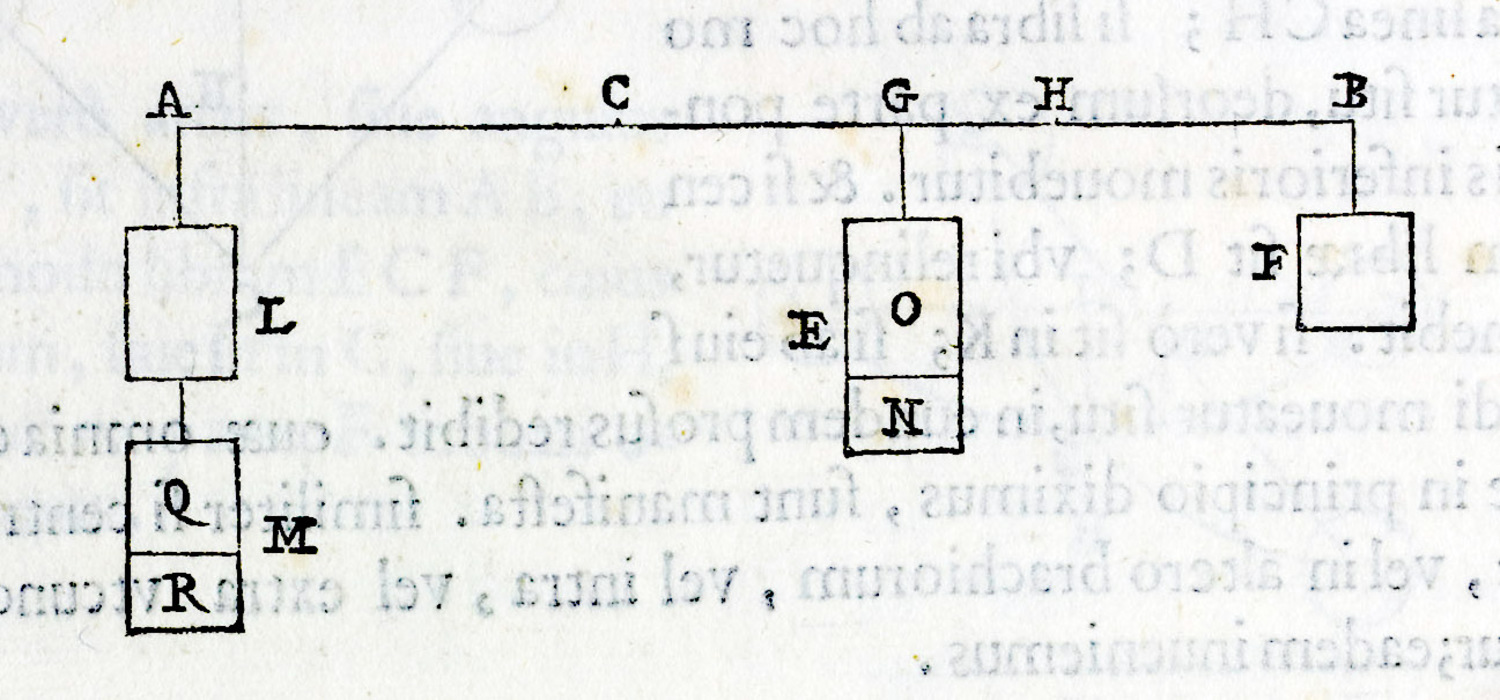
Fig. 3.2: Balance AB with center C and with weights E and F attached according to the fifth proposition in order to compare their effect in dependence of hanging from points G and B, and after being moved together at point H
In contrast to Archimedes in his treatise On the equilibrium of planes, Guidobaldo does not compare weights attached to the two sides of a balance in equilibrium, but rather compares the effect of two weights hanging down from two points on one side of the beam and their effect after both are moved to a point in between. The proportion between the two weights (pondera) is first conceived as the proportion between their actual weights. But the verb “to weigh” (ponderare) cannot mean the same here. Since a weight remains constant wherever it is placed, the statement of the proposition taken literally seems to be nonsensical. The terms pondus and ponderare are obviously used here within one and the same proposition with two different meanings, the latter designating the varying effect of the weights moved to different positions rather than their actual weights.
Guidobaldo provides a long and clumsy proof of this proposition which from a modern point of view is a simple consequence of the law of the lever. Here, however, this proposition is used rather to prove the law of the lever for the special case of the steelyard with its moving weight.
This law is the subject of the sixth proposition. Guidobaldo claims that:
Equal weights (pondera) attached to a balance have proportions in gravity (in gravitate proportionem habere) as the distances (from the center) at which they are attached.22
Here Guidobaldo uses the distinction between weight (pondus) and gravity (gravitas) in order to express that the effect of a weight differs according to the distance from the center. Again the proof is complex, missing the elegance of the ancient proof of Archimedes whom Guidobaldo so admired.
The final seventh proposition provides the construction of the point on a beam at which it has to be supported to bring it into equilibrium if a number of different weights are attached to different places on the beam of a balance.
3.5 The Chapter De Vecte
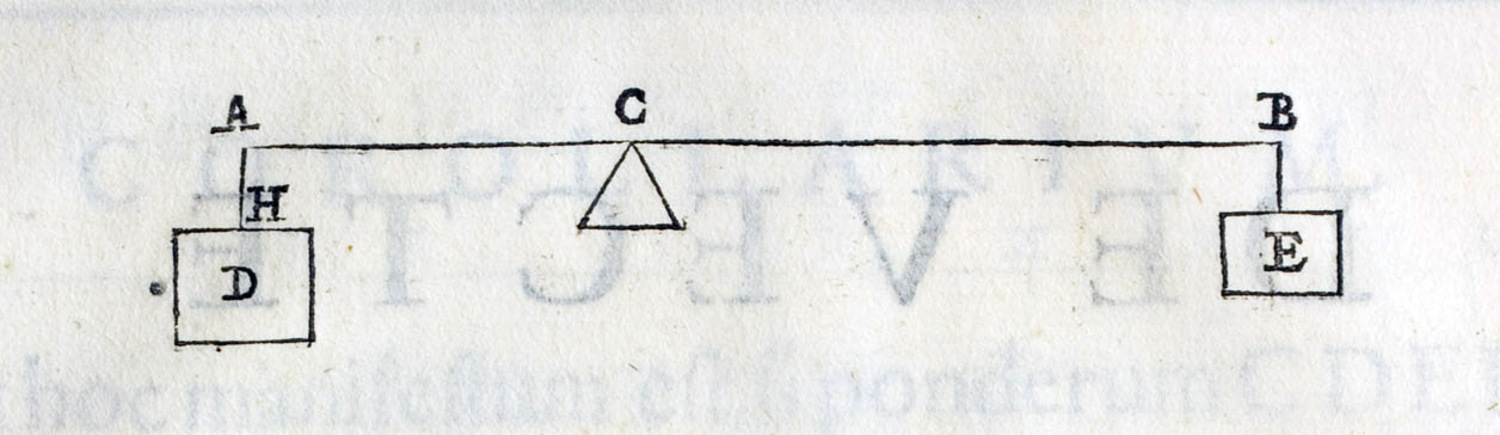
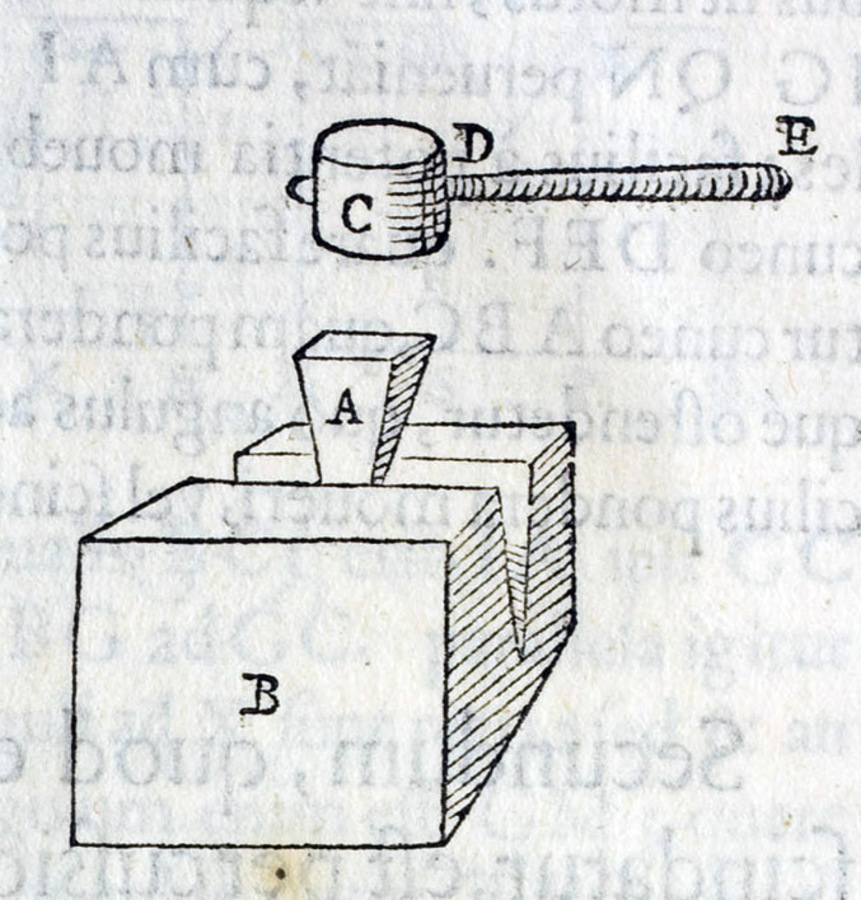
Fig. 3.3: The lever (vecte) with a weight D (pondus) hanging down from the beam at A fastened by AH. The weight is compensated by a force E (potentia) acting at point B
From a modern point of view, there is no substantial difference between a balance with unequal arms, that is, a steelyard (statera), and a lever. Guidobaldo, however, treats them in different chapters. He added, as a sixth, the balance to the five simple machines of Heron, discussing it separately in the initial chapter before dealing with the lever in the following chapter.23
The reason may be that he followed the theoretical program promoted by the Aristotelian Problemata mechanica which, as mentioned earlier, was well known and frequently commented on in the 16th and 17th centuries.24 According to this treatise, the function of mechanical devices, which has to be explained, is to reduce the required forces:
When, then, we have to produce an effect contrary to nature, we are at a loss, because of the difficulty, and require skill (techn√™, œÑŒ≠œáŒΩŒ∑). Therefore we call that part of skill which assists such difficulties, a device (m√™chan√™, ŒºŒ∑œáŒ±ŒΩŒÆ). For as the poet Antiphon wrote, this is true: “We by skill gain mastery over things in which we are conquered by nature.” Of this kind are those in which the less master the greater, and things possessing little weight move heavy weights, and all similar devices which we term mechanical problems.25
According to the Aristotelian program, this functioning of mechanical devices has to be traced back to the functioning of the lever, which itself has to be traced back to the functioning of the balance, and which in turn is explained by the miraculous properties of the circle:
... there is nothing strange in the circle being the first of all marvels. The facts about the balance depend upon the circle, and those about the lever upon the balance, while nearly all the other problems of mechanical movement can depend upon the lever.26
Thus, by putting his own chapter on the balance before his chapters on the simple machines, Guidobaldo simply merges the theoretical programs of Heron and of the author of the Aristotelian treatise, who may or may not have been Aristotle himself.
The terminology used in Guidobaldo's chapter on the lever differs from that of the previous chapter on the balance. The center of the balance is replaced by the term fulcimentum. More important is the fact that there are not only weights (pondus), but also forces (potentia) acting on the lever. This latter distinction mitigates the problem of distinguishing between the actual weight of a body and the effect it has at a certain distance from the fulcimentum, designated now as its potentia.
Guidobaldo's chapter on the lever, following the chapter on the balance, again starts with a lemma and contains a further fifteen propositions. Like the lemma at the beginning of the chapter on the balance, the lemma at the beginning of the chapter on the lever is also purely mathematical, in this case dealing with proportions.
The following first proposition states the law of the lever, and thus corresponds to the sixth proposition on the balance. It is now phrased with the changed terminology:
The force (potentia) sustaining (sustinens) a weight (pondus) attached to a lever has the same proportion to the weight as the distance on the lever between the fulcimentum and the suspension of the weight to the distance from the fulcimentum to the intervening force (potentia).27
The following second and third propositions deal with different constellations of weights and forces acting on a lever.
The fourth proposition states that if a weight is moved by a force acting on a lever, the spaces (spatio) traversed by the force and the weight are in the same proportion as the distances to the fulcimentum.
The following fifth to tenth propositions (including the sixth and seventh propositions, which are geometrical auxiliary propositions) are related to the problem to determine the effect of forces on weights to be moved depending on the position of the center of gravity above, below or in line with the lever. Guidobaldo assumes that the vertical projection of the center of gravity to the lever, whether in horizontal or oblique position, determines the point on the lever to be taken in account as the distance to the fulcimentum. While in the case of a horizontal position of the lever this procedure provides a correct result, in the case of an oblique position of the lever, the result is ambiguous, since Guidobaldo disregards the differing effect of the direction (either vertical to the horizon or to the lever) of the applied force.
The eleventh to fourteenth propositions draw conclusions concerning the determination of forces that can move weights by means of a lever if certain constellations are given.
All propositions so far are proven under the assumption that the balance or the lever are themselves weightless. The final fifteenth proposition now raises the problem of how the weight of a material beam has to be taken in account. This problem was well known and solved in the Arabic tradition, if not already in antiquity. Guidobaldo's fifteenth proposition provides an answer for the simplest case of one weight attached to a material beam with a given weight.
3.6 The Chapter De Trochlea
The chapter entitled De Trochlea28 contains a systematic theory of pulley blocks. It starts with an explanation of the relation between a weight (pondus) to be lifted and the force (potentia) required to suspend it using a single pulley. In the following, pulley blocks (trochlea) with increasing complexity containing different arrangements of up to six pulleys are investigated.
The main goal of the chapter is to reduce the functionality of different mechanisms of such pulley blocks to the functionality of the lever and thus to apply propositions proven for the lever to the explanation of the effect of using pulleys. Guidobaldo uses an ingenious method for accomplishing this program, combining levers in order to construct models of pulley blocks with the same functionality. He then proves each proposition for each type of pulley block, first for the lever model, and then transfers the result to the pulley block itself.
The chapter contains altogether twenty-eight propositions. It starts with a short introduction explaining the construction of a pulley block and alluding to the Collectiones of Pappus and to the Tenth Book of the Architectura of Vitruvius29 as ancient sources discussing the use of pulleys for the construction of such pulley blocks. He also implicitly alludes to the Aristotelian treatise Problemata mechanica by quoting almost literally its basic goal of theoretical explanation, that is, to explain why a small force can move a large weight:
Furthermore, the moving force may be placed at G, so that, as long as it descends, A will be raised up in opposite direction, just as Pappus shows in the eighth book of the Mathematicae collectiones and Vitruvius in the tenth of the Architectura, and others.
We show, moreover, how this instrument pulley can be reduced to the lever, why a large weight (magnum pondus) can be moved by a small force (ab exigua virtute), and how, and in how much time ...30
Guidobaldo again starts with a purely mathematical lemma, this time concerning a simple geometrical figure with parallel tangents to a circle. The following propositions representing Guidobaldo's theory can be divided into four groups.
The first group consists of the first to tenth propositions. These propositions serve to determine the force (potentia) required to suspend a given weight by means of a growing complexity of pulley blocks. Among these propositions, the fourth, sixth, and eighth propositions deal with the lever models for pulley blocks.
The second group consists of the eleventh, thirteenth, fourteenth, and sixteenth propositions. These serve to determine for different pulley blocks the space the force has to pass through in order to move a weight through a certain distance.
The third group containing the twelfth, fifteenth and seventeenth to twenty-sixth propositions returns to the program of the first group. The force required to suspend a weight is determined for further complex types of pulley blocks.
Finally, the twenty-seventh and twenty-eighth propositions solve the problem of moving by means of a pulley block a given weight with a given force, and of moving a weight through a given distance with a force applied over a given distance.
3.7 The Chapter De Axe in peritrochio
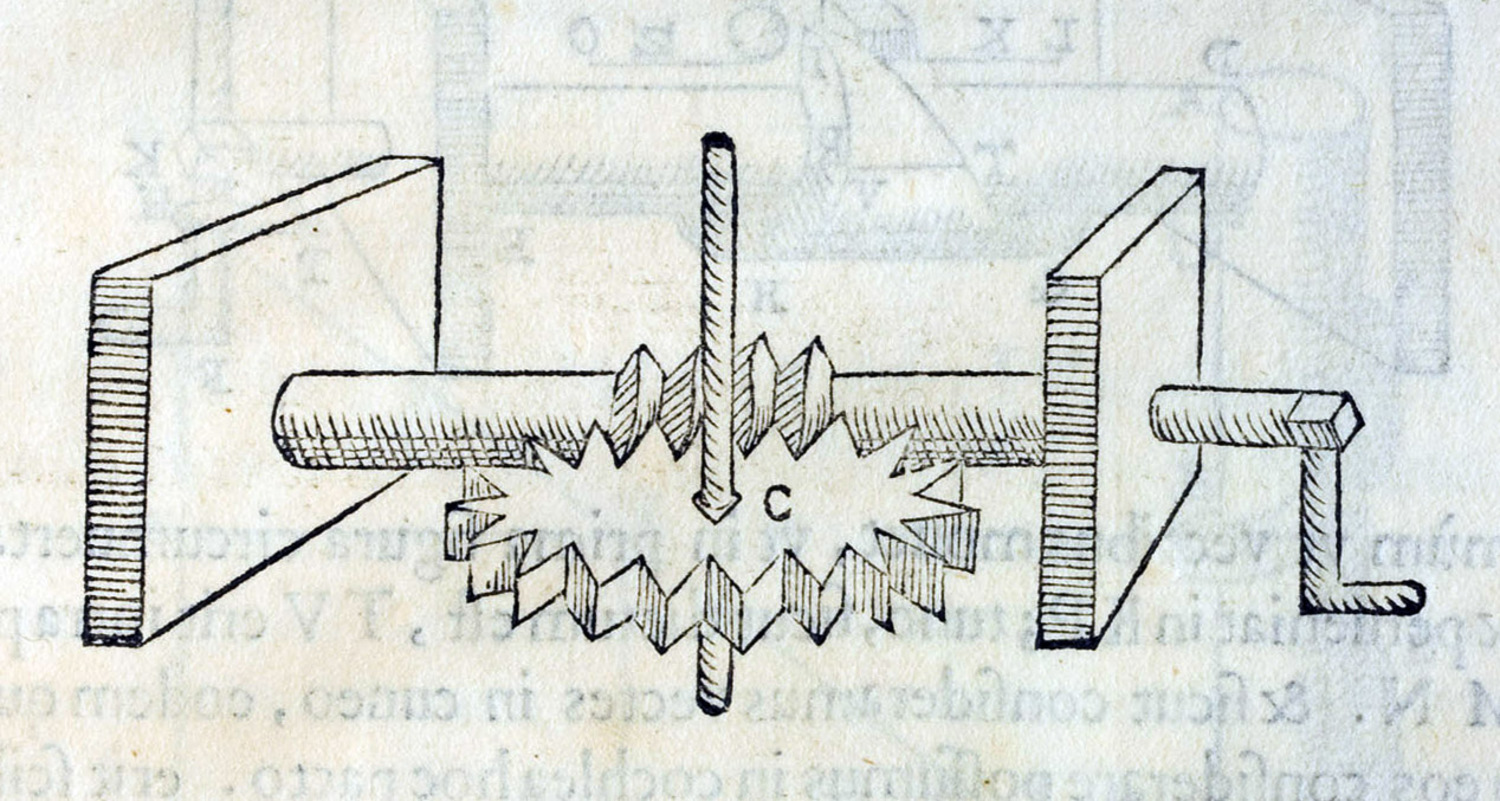
Guidobaldo begins the chapter concerning the wheel attached to an axle31 again with reference to its ancient origin. He says that this instrument was already described by Pappus in his Mathematicae collectiones. Then, some designations of parts of the instrument are explained, terms for the axle (axe), the drum (tympanum), the handles (scytala), the force acting on the handles (potentia), the weight (pondus) which is moved up, and the rope (fune) around the axle which suspends the weight.
Also in this chapter, alluding to the Aristotelian Problemata mechanica, its goal is explicitly stated:
Therefore it remains for us that we exhibit why, by means of this instrument, large weights (pondera) can be moved by a small force (ab exigua virtute) and also in what way; moreover that we show the ratio of the time and the space, (and) in turn of the moving force moventis ...potentiae and of the moved weight moti ponderis; and that we reduce such use of the instrument to the lever.32
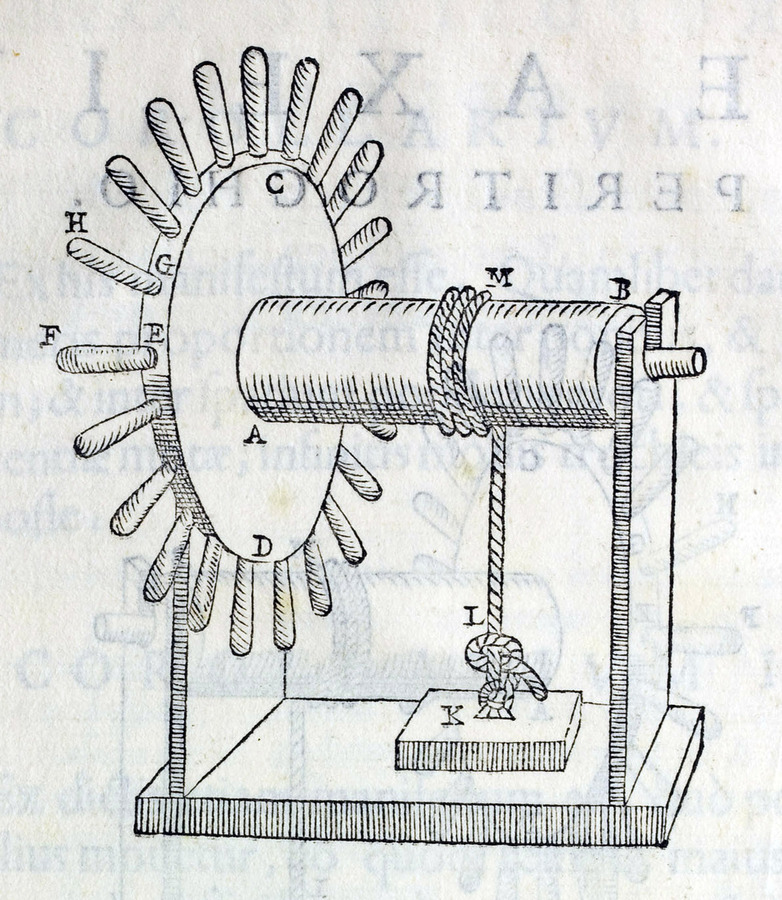
Fig. 3.5: The axle in a wheel (axe in peritrochio) with the axle AB, the drum CD, the handles EF, GH etc., the places F, G etc. where the force is applied, the weight K to be moved up, and the rope LM around the axle which suspends the weight
This introductory note is followed by two propositions only. The first proposition states that the force (potentia) sustaining the weight (pondus) has the same proportion to the weight as the radius of the axle to the radius of the the drum (tympanum) together with the handles (scytala). The second proposition solves the problem of determining for a given weight (pondus) and force (potentia) the wheel (axe in peritrochio) by which it is moved.
The chapter ends with a remark about instruments that can be considered as examples of the described wheel. The instruments explicitly named are a sort of capstan or windlass (ergata), a type of winch (succula), the borer (terebra), and the wheel with its axle (tympanum cum sui axibus), whether teethed (dentatus) or not.
3.8 The Chapter De Cuneo
The chapter on the wedge33 differs from the previous ones insofar as it contains no propositions that are explicitly labeled as such. It starts instead with a reference to the treatment of the wedge in the Aristotelian treatise Problemata mechanica34 which in fact is the basis of Guidobaldo's treatment of the wedge. In particular, Guidobaldo adopts the idea that the two flanks of a wedge can split other material because they act as two levers.
IIn what follows, he discusses in detail the different possibilities of identifying the location that is considered as the fulcimentum, that is, the place which has to be interpreted as the unmoved point around which the lever turns. Furthermore, Guidobaldo claims that the flanks of the wedge can also be considered as inclined planes which in turn can again be reduced to the lever in order to explain their effect. In particular, he argues that the more acute the angle of the wedge is, the more easily it moves and splits the wedge. He then discusses the problem that the impact of strokes is a further condition for more easily moving the wedge and splitting its object.
n the course of this discussion certain EOAemphasized statements seem to be meant as propositions, but are not explicitly designated in this way. The justifications for several of these statements end with phrases typically ending the proof of a proposition, phrases such as quod demonstrare oportebat. In one case, such an implicit proposition is followed by a corollarium, explicitly designated as such.
The statements justified in this way are only qualitative in nature throughout. In the case of reducing the wedge to the lever, this is a consequence of Guidobaldo's neglect of the directions in which forces act. In the case of interpreting the flanks of the wedge as inclined planes, no quantitative statement is possible because Guidobaldo follows the fallacious theory of Pappus in his Mathematicae collectiones.35 Finally, in the case of the role of percussion there was no theory available to Guidobaldo that allowed for a calculation of the relation between force and effect.
3.9 The Chapter De Cochlea
The final chapter on the screw36 again begins with reference to the Mathematicae collectiones of Pappus.37 Guidobaldo claims that, while Pappus explained how to build a screw for moving heavy weights and attempted to explain the screw as acting like a wedge without percussion and thus moving by means of a lever, he nevertheless did not supply an adequate explanation. He himself therefore formulates as the goal of his chapter the provision of this missing explanation and a demonstration of the effect of the screw as a wedge. He would thus eventually reduce the screw to the lever and the balance.
Guidobaldo describes in detail the possible effect of a wedge coiled around an axle. By turning the axle the wedge can split an appropriately fixed block. Guidobaldo then continues with two propositions.
In the first proposition, he claims that a wedge, appropriately coiled twice around an axle, can be interpreted as a screw with two threads. He shows in his proof that such an axle coiled with a wedge can move a block, instead of splitting it, if it is guided along a support. He then describes in detail various instruments using a screw and explains how they work. Finally, he applies to the screw his interpretation of the wedge acting like a lever.
The second proposition is based on the interpretation of the wedge acting like an inclined plane. Guidobaldo claims in this proposition that also an inclined plane coiled around an axle can be interpreted as a screw.
Having proven this proposition, he adds the remark that the screw can thus be reduced to the balance (ad libram reducatur) according to Proposition IX of Book VIII of Pappus' Mathematicae collectiones38 without noticing the falsity of the argument. As mentioned above, Pappus' identification of the inclined plane with a lever is incorrect, not only from the viewpoint of later classical mechanics, but also due to its inherent consequence that increasing the angle of an inclined plane towards the vertical would infinitely increase the force required to lift a body up, which is incompatible with any experience of lifting weights.
Guidobaldo continues again with a discussion of various instruments that use a screw, now interpreting them as based on the inclined plane. From the interpretation of the screw as a coiled inclined plane, he derives the consequence that the greater the number of threads within a length unit and the longer the handles, the more easily and slowly the weight will be moved.
Finally, Guidobaldo argues that only in the case of the application of a lever can a precise proportion between the suspending force and the suspended weight be determined. In all other cases, intervening factors such as the length of the handles of a wheel or the strength of the stroke applied to a wedge modifies the proportion. This discussion serves to justify the restriction to qualitative statements about the relation of force and weight when these instruments were analyzed.
Footnotes
See Alexandria 1900, 95.
See Alexandria 1660, 460, mentioned at the beginning of the proof of Proposition X of Book VIII. Commandino's translation of Books III to VIII was first published posthumously in 1588 under the title Mathematicae collectiones. A later edition is used here; see Alexandria 1660. The final editing was done by Guidobaldo who surely had access to the Greek text and to Commandino's translation long before his death in 1575. Commandino had already published translations of excerpts of Pappus' text in his editions of Perga 1566 and of Samos 1572, that is, at the time Guidobaldo stayed with him as his private disciple.
See Alexandria 1900, 94 and the corresponding order of the subsequent treatment of the simple machines.
See Alexandria 1871, 311.
It is commonly accepted that the treatise of Archimedes 1953, 189-220 On the equilibrium of planes is only part of a lost corpus of Archimedes' work on mechanics: Heron refers three times to specific works, see Alexandria 1900, 64-66, 70, and 86-88. In the present context he mentions a work dealing with the equilibrium of figures to which a lever is applied. This may refer to the extant treatise On the equilibrium of planes, however, this treatise does not contain a definition of the center of gravity. The other two remarks of Heron about works of Archimedes refer to titles which cannot be identified with extant works of Archimedes, a Book on pillars and Treatises on the lever. See the discussion of the lost works of Archimedes and in particular of the unknown definition of the center of gravity by Archimedes in Dijksterhuis 1956, 47f. and 295-304.
Girolamo Cardano, 1501-1576.
Monte 1577, 30v; translation by the authors.
Monte 1577, 34r; translation by the authors.
For a detailed analysis of the role of this treatise, see (Rose and Drake 1971).
Monte 1577, 34r; translation by the authors.
Marcus Vitruvius Pollio, first cent. BCE.
Monte 1577, 62v; translation by the authors.
Monte 1577, 106v; translation by the authors.
Problem 17, see Aristotle 1980, 371.
Pappus' theory of the relation between the weight of an object and the force required to prevent it from sliding down an inclined plane has its roots in the Mechanika of Alexandria 1900, 60-62. Heron's argument, while presented as being valid for any object placed on an inclined plane, concerns only a rolling cylinder and is, at best, only qualitatively correct and only for a rolling body. He interprets the rolling cylinder as a lever turning around the point of contact between the cylinder and the inclined plane, however, comparing only the weights on both sides of the vertical through the center of the lever without taking into account the distances of the centers of gravity of both parts from this vertical. Alexandria 1871, 326-331 tried to improve the argument but actually made it worse. His sophisticated identification of a rolling sphere with a lever is totally untenable. As Drake and Drabkin 1969, 325 noted, this has implications that are not even qualitatively correct. According to his argument the force required to compensate the weight of the sphere when the inclined plane is steepened towards the vertical increases to infinity and not, as it should be, to the actual weight of the sphere.