Bryce DeWitt recalls having a conversation with Pauli in 1949, at the Institute for Advanced Study, in which Pauli asked him what he was working on,1 to which DeWitt responded: “trying to quantize the gravitational field.” Pauli was something of a veteran of quantum gravity by this time. His response, after shaking and nodding his head a few times (“die Paulibewegung”), was: “That is a very important problem—but it will take someone really smart!”.2 More than half a century since this conversation, and with the work of many genuinely “really smart” people (including several geniuses), the problem has, of course, not yet been resolved. Yet still the field has accumulated a rich and interesting past that has yet to be properly studied. It has become customary to mark a certain stage of maturity of a theory by producing a volume of sources of early papers from which that maturity emerged.
Though quantum gravity has not yet achieved full scientific maturity, it has at least achieved chronological maturity, with almost a century of struggle behind it. Therefore, we feel it is entirely appropriate to treat this old timer with some respect, of which it has not received all that much from the history of physics. A volume providing a historical overview, after so long without one, can be beneficial to the current and future generation of physicists working on the problem, in order to see how far research on the problem (and the way the very problem itself is conceptualized) has come—this further provides a fresh perspective on what still remains to be done. It might point to further refinements of how we understand the problem so that it can finally be resolved.
As Julian Schwinger pointed out in the preface to his own collection of papers from the history of quantum electrodynamics,3 any such selection of sources is bound to reflect the particular viewpoint of the editor(s). Following Schwinger, we briefly describe our “selection process.” Despite the fact that the period we cover spans only 35 years, it was necessary to be fairly brutal in rejecting papers for which a case for inclusion could easily be made. Likewise, it is likely that cases could be made for excluding many of the papers we decided to include. The point is, the sources chosen are an imperfect reflection of the development of a field, and one important reason for this is that “the field” in question has always been somewhat slippery and hard to define, but especially so in its earliest phases of development. One can’t, for example, point to particular phenomena that the theory will describe since any such phenomena would be experimentally and observationally very remote. Moreover, in the earliest phases of research, the ingredient theories (general relativity and quantum mechanics) were themselves still being worked through and, in the case of the latter, were not properly formulated for some time (as Part I indicates). Thus one finds the definition of the problem of quantum gravity is non-stationary on account of being largely at the mercy of wider developments in quantum mechanics and general relativity in our chosen time period—one sees this especially clearly in Part II, but it is really a general feature.
Firstly, let us explain the period we have restricted our sources to, namely <1950. This is a relatively short snapshot of history, but it has the advantage of revealing the steps taken before the rather dramatic explosion of work in the 1950s—this explosion was due to a variety of factors beyond internal advances in physics, including the emergence of new schools of research in general relativity (especially Peter Bergmann’s, Hermann Bondi’s, Alfred Schild’s, Leopold Infeld’s, and John Wheeler’s) and new sources of funding (especially the NSF, the ONR, and other military and philanthropic programmes).4 We also find that the pre-1950 research already includes many of the main lines of attack and the main general arguments for (and against) quantization. Focusing in on the very earliest period sharpens the physical intuitions behind the various choices (of formalism, terminology, and more) that have since been assimilated or forgotten.
We will now go on to explain why there are papers in here (many, in fact) that are not strictly “quantum gravitational”. One can quite usefully think of the development of research programmes (and questions) in a field in terms of “evolutionary trees.” Pursuing this in the case of organisms eventually leads one outside of the species of interest. Or one might find branch points, in which now divergent organisms converge onto a common ancestor. Likewise with the evolution of a field of inquiry. Since this is a “sourcebook”, rather than a straight history, we are guided by our present day theories and approaches, and so are more concerned with tracing back various ancestors. Some of these ancestors look like the present day approaches, and others don’t. But regardless of which is the case, they have nonetheless been involved in the development of the present approaches. Hence, we have often erred on the side of being too liberal where ideas that originated in a slightly different context were nonetheless incorporated into quantum gravity research at some later date.
Quantum gravity is, of course, yet to be articulated in any final, agreed upon formulation. As alluded to above, with new developments in physics, the quantum gravity project would attempt to avail itself of some potentially relevant feature—it is, thus, a “parasitic” enterprise for much of its early history: wave mechanics, spin and the Dirac equation, neutrinos, the discovery of new forces, mesons and cosmic rays, ... . All of these and more were immediately taken up as of potential relevance in quantum gravity’s definition and domain. Parts I and II study the ways in which quantum gravity was studied in its embryonic and infancy stages. In cases where it is not parasitic, it is viewed not so much as a problem in its own right, but as an interesting case study, or else a resource to cure problems in field theory more generally (the “more serious” business of physics). For example, in 1938 one can find Born writing that there “seems to be a general conviction that the difficulties of our present theory of ultimate particles and nuclear phenomena (the infinite values of the self energy, the zero energy and other quantities) are connected with the problem of merging quantum theory and [general] relativity into a consistent unit”.5 Parts III and IV cover such aspects. Part III also deals more generally with the direct quantization of general relativity using techniques that had been applied to the electromagnetic field.
What is interesting about these early papers, in terms of the “shut up and calculate” narrative that is often told about physics after the war, is that the papers very rarely step into conceptual waters. One can find none of the preoccupation with the status of observables, the existence of space and time, the meaning of diffeomorphism symmetry, and other such foundational problems that spring up in the 1950s—almost immediately where the papers in this volume stop, in fact. To a certain extent this later development had to do with physicists stepping back and considering the classical theory of general relativity more carefully from a physical point of view than had been done previously. The reasons for this are clear: the standard techniques faced technical problems of their own. There was a dawning recognition, towards the end of the first half of the twentieth century, that gravity was simply not like other forces.6 This recognition brought with it the idea that the problem of quantum gravity will most likely not be resolved through a purely technical solution.
Footnotes
DeWitt (then still using the name Carl Bryce Seligman) had only just finished his doctoral thesis on quantum gravity (under Julian Schwinger at Harvard: submitted in December, 1949), and was interested in the possibility of a postdoc at ETH.
“Quantum Gravity: Yesterday and Today.” General Relativity and Gravitation 41, 2009: p. 414.
Selected Papers on Quantum Electrodynamics (Dover, 1958).
In the historical literature of general relativity it is known as “the renaissance of GR”—see, e.g., Jean Eisenstaedt’s “The Low Water Mark of General Relativity, 1925–1955” (in D. Howard and J. Stachel, eds., Einstein and the History of General Relativity, Birkhäuser, 1989: 277–292), David Kaiser, “A
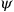 is just a
is just a
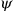 ? Pedagogy, Practice, and the Reconstitution of General Relativity, 1942-1975” (Studies in History and Philosophy of Modern Physics 29, 1998: 321–338), and AB, Roberto Lalli, and Jürgen Renn, “The Reinvention of General Relativity: A Historiographical Framework for Assessing One Hundred Years of Curved Space-time” (Isis 106, 2015: 598–620).
? Pedagogy, Practice, and the Reconstitution of General Relativity, 1942-1975” (Studies in History and Philosophy of Modern Physics 29, 1998: 321–338), and AB, Roberto Lalli, and Jürgen Renn, “The Reinvention of General Relativity: A Historiographical Framework for Assessing One Hundred Years of Curved Space-time” (Isis 106, 2015: 598–620).
“A Suggestion for Unifying Quantum Theory and Relativity.” Proceedings of the Royal Society London A 165(921), 1938: p. 291. By this stage, Born was thinking of the problem as involving the mixing of quantum principles with the principle of general covariance, rather than general relativity more broadly conceived—this on account of the fact that “gravitation by its order of magnitude is a molar effect and applies only to masses in bulk, not to the ultimate particles.” However, the idea that general relativity might be employed as part of the basic framework of a future theory of elementary particles became popular in later work.
We see the sources of this in Part V in which the general covariance of general relativity was tackled head on in the context of a parameter formalism and the constrained Hamiltonian formulation.
