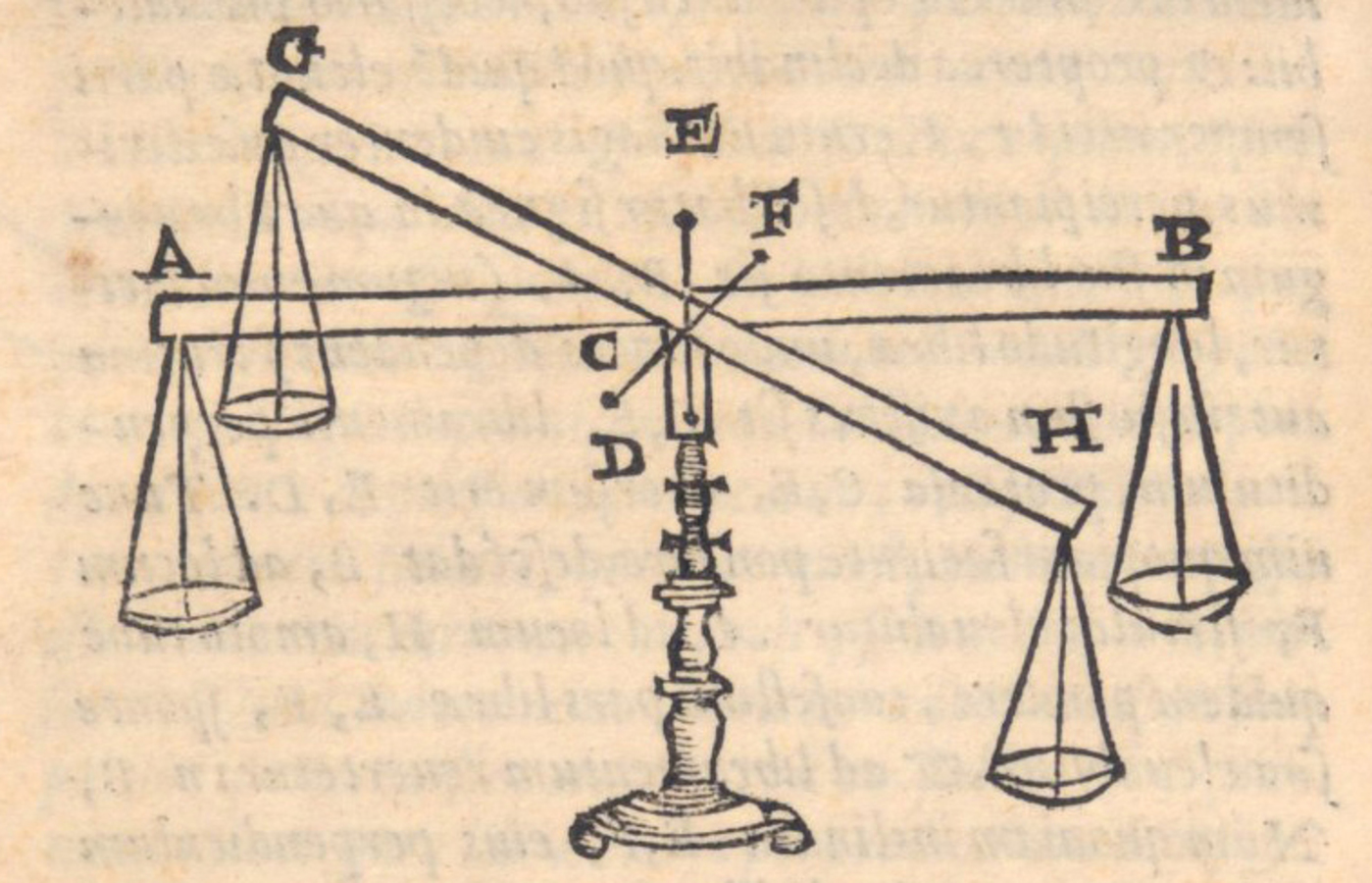
Fig. 1.1: Illustration of an equal-armed balance, both in equilibrium and in a deflected position. From Piccolomini 1565.
1.1 On this book
Since ancient times, scales have symbolized justice and equilibrium. Balance and equilibrium in this wider sense are fundamental to the human condition, but what about the real, physical balance and its equilibrium? This book is not concerned with the balance between humanity and its natural environment, or with an equilibrium of power or of the human mind, but rather a seemingly innocent question concerning the real balance: the question of whether a balance in equilibrium, after having been deflected from its normal horizontal position, remains in its deflected position, returns to its original position, or tilts to the vertical. This question is of no immediate practical relevance – although it may affect the reliability of a balance – and is certainly not of fundamental significance to the human condition. Nevertheless, it captured the attention of philosophers, scholars, engineers, and scientists for almost two millennia, from Greek antiquity to the sixteenth century when this question became central among scholars and the subject of what we call here the equilibrium controversy. However, a conclusive answer was not found until the firm establishment of classical physics, and even then there were still aspects that provoked controversial discussions.
But why should anyone be interested in such a seemingly trivial and irrelevant issue? One can hardly avoid the impression that scientific investigations – and historical scholarship in particular – dedicated to such issues are inconsequential and detached from human endeavors. Today, of course, science is surely not removed from the human condition, but is actually critical for human survival. But this science is concerned with the grand challenges of humanity such as deciphering and interpreting the human genome, solving the energy problem, or overcoming the climate crisis. On closer inspection, however, all such pursuits are rooted in scientific knowledge that originated in intellectual concerns as remote from immediate practical applicability as the equilibrium controversy. There would be no scientific understanding of energy without the pivotal role once played by the balance and its equilibrium in understanding this concept.
The question of whether or not an equilibrated balance, deflected from its standard position, would return to the horizontal position, appears to be a typical textbook problem. In real life, most balances do return to their original position, so clearly we must be talking about an idealized balance that can be visualized, for instance, by an immaterial beam, suspended at its center, with two equal weights attached to its ends. Or we may imagine the more complex case in which the beam is extended, has itself weight, and is suspended above or below its center. All such cases can be solved with the techniques of classical mechanics, for instance, by introducing the concept of center of gravity, by conceiving of one arm of a deflected balance as an angular or bent lever, and by using the concept of torque in order to establish the effects that the forces exerted by the weights have in different positions along the balance.
Why then was it so difficult to resolve this question? Can a few simple experiments not settle the issue? The answer to such elementary questions about the progress of physics can only be found if we take into account the role that the historical development of fundamental concepts such as force, weight, center of gravity, and torque have played for the understanding of seemingly simple physical problems, such as those that formed part of the equilibrium controversy. The nature of the historical evolution of mechanical knowledge, as the subject of an historical epistemology, can only be understood if one realizes that this evolution is not a linear process, but rather involves extensive restructurations of knowledge accompanied by concept development in the sciences that deal with this knowledge.
The fundamental concepts of mechanics have a very long history. They have roots in antiquity and were – or so it seemed – definitively clarified in the classical physics of the eighteenth and nineteenth centuries. But then it turned out that in the course of the relativity and quantum revolutions of the early twentieth century, even such apparently basic concepts were subject to further profound modifications. Against the background of these conceptual revisions, even a simple problem such as that of the bent lever, for instance, could in fact once again become a challenging issue, although it had apparently been firmly established in the course of the equilibrium controversy of the sixteenth century. A genuine understanding of the bent lever in relativity could not simply be accomplished with the help of the classical concepts of force and torque, but actually necessitated a reconceptualization of the relation between energy and momentum from a relativistic perspective.1
Nevertheless, concepts with roots in antiquity such as force, weight, center of gravity, and torque continue to serve as important points of reference, even for modern physics. How did these concepts emerge? Did they perhaps result from the establishment of a definitive scientific method, which is often associated with the Scientific Revolution, an era in which the equilibrium controversy culminated and classical mechanics emerged? But why then did these concepts undergo further changes in the subsequent revolutions of physics? The present book aims to contribute to the understanding of the fundamental role of concept development for science by focusing on one particular example, by providing some relevant historical contexts, and by highlighting the specific role that scientific controversies and challenging objects played in this development.
Classical mechanics is often considered to be the most pure, abstract, and rational of the physical sciences.2 It is hence natural to assume that its historical development must also have been essentially a history of linear progress, or at least of the steady accumulation of knowledge. This may have suffered interruptions and aberrations, but it nevertheless tended to reach clear conceptual foundations based on the consideration of idealized objects such as the balance described above. One aspect that will become particularly evident in this book is the role historical contingencies played for conceptual development at the heart of mechanics. There is, first of all, the contingency of those aspects of the material culture that become the object of scientific enquiry. These could include the balance, the pendulum, an elixir, or even the shadow of a gnomon. Then there is the contingency of the social and cultural conditions under which knowledge is recorded, transmitted, and appropriated, including the losses and transmutations occurring in such processes. Here we will show that such losses and transmutations not only acted as disturbances in an otherwise linear progress toward clarity, but that they also determined, to a large extent, the very nature of concept development in mechanics. Naturally, there is also the contingency inherent in the very processes of knowledge generation as knowledge itself is characterized by a complex cognitive architecture that gives rise to unpredictable twists in its development, as is familiar from other aspects of cultural evolution. And finally, there is the contingency that itself becomes the object of scientific reflection, for instance, in the form of the question of which material processes can be studied with scientific rigor and which must be excluded from the realm of mechanics because they are not subject to precise mathematical laws.
No doubt, science is a deeply human affair, historical down to its very core concepts. Perhaps there is no need for further study to illustrate that nothing that is human is alien to science. But is not the question of how the specific features that distinguish science from other social activities still a challenging intellectual problem? In particular, how can science ensure the long-term proliferation of knowledge while undergoing, at the same time, profound conceptual transformations as we have indicated? What role is played by the material culture underlying science as a social activity, and what significance does the long-term transmission of theoretical traditions have, and how is concept formation affected by different social and cultural contexts? In order to answer such questions, we propose that it makes sense to imitate science itself, that is, to start not necessarily from what are perhaps the most interesting, complex, and advanced forms of the phenomenon to be studied, but rather to take a simple but characteristic model case, such as the concept development taking place in the context of the equilibrium controversy.
Finally, a personal note: When Peter Damerow and I began to work on this book some three years ago, questions such as these were pertinent, but did not present the primary goal of our enterprise. Our principal aim was rather to make available to a wider public an important new source on the history of mechanics, a source that illuminates a critical phase of the equilibrium controversy: the handwritten marginal commentaries by one important early modern author on the book of another contemporary author. Our intention was to reserve theoretical issues of historical epistemology such as the questions listed above for a comprehensive study of the evolution of mechanical knowledge. It was only in the course of our efforts to understand the pre-history and contexts of the sources that the equilibrium controversy presented itself as a perfect illustration of some of the theoretical insights into the nature of the evolution of the knowledge under consideration.
This book began as an edition of new historical sources, but was transformed over time into a case study of the long-term history of mechanical knowledge. Yet, in accordance with the scope of the series, the sources remain at center stage, while the theoretical passages take more the form of commentaries and excursions than of systematic studies. Wherever feasible and useful, we have included quotations both in the original language and in English translation. We furthermore extensively used, as in the other volumes of this series, the digital library of the ECHO initiative, which makes many of the relevant historical materials freely accessible on the Web. We also included hitherto unpublished results of earlier work, pursued in the context of the research project Mental Models in the History of Mechanics at the Max Planck Institute for the History of Science.
As in other joint projects, Peter and I worked closely on every sentence until the book was almost finished. Even when Peter's struggle with his illness became ever more hopeless, he continued to work with the greatest intensity on this project. He carefully economized his last resources to be able to make final revisions and improvements. I have never known anyone so dedicated, so serene and cooperative, and so ingenious, even in the face of death. His mind and heart were stronger than any bodily weakness. He literally worked on this joint project until his very last moment and it hurts to think how much he would have liked to see it completed. It is therefore with the greatest respect for my friend and co-author that I have tried to implement the final amendments as far as possible and rush in making this, his last work, available in the open-access series that Peter initiated.
This would not have been possible without the continuing support of several colleagues. I am therefore particularly grateful to Lindy Divarci who looked after this project from the beginning, to Beatrice Gabriel who kept encouraging us and carefully copy-edited the final version, to Urs Schoepflin who helped to track down many of the sources, to Sabine Bertram for her help with the ink analysis, as well as to the development team, including Jörg Kantel and Kai Surendorf, for realizing the online version. Some of the transcriptions and translations have been corroborated by Eleonora Renn, Volkmar Schüller, and Stefan Trzeciok. We are particularly grateful to Antonio Becchi, Carlo Maccagni, and Pietro Daniel Omodeo for their extensive help with checking transcriptions and translations and for acting as critical and helpful submitters and reviewers, to Gideon Freudenthal for important suggestions on some of the theoretical passages, to Alexander S. Blum for his help in presenting the physics, and to Jochen Büttner, Peter McLaughlin, Matthias Schemmel, and Matteo Valleriani for many discussions in the framework of our joint research on the history of mechanics. Discussions with Horst Bredekamp always provided a strong motivation to see the project to its end. We would also like to thank Martin Frank, Enrico Gamba, and Pier Daniele Napolitani for many productive discussions of this material and for their collaboration in the context of the project Archimede nel Rinascimento: Laboratorio Urbino 1500. Parts of this work were written during a stay of one of us (J. Renn) at the Einstein Papers Project at the California Institute of Technology in Pasadena. We especially acknowledge the constant support of Rivka Feldhay and Paolo Galluzzi as members of the Scientific Advisory Board of the Max Planck Institute for the History of Science, and also the support received by the German Israeli Foundation (GIF) in the framework of the Project From Knowledge and Faith to Science and Religion: The Jesuit Way to Modernity. And finally we gladly acknowledge the stimulating context that the Collaborative Research Center Transformations of Antiquity under the direction of Hartmut Böhme and the project TOPOI – The Formation and Transformation of Space and Knowledge in Ancient Civilizations have provided for this work.
Jürgen Renn, December 2011
1.2 A first glimpse at a new document
In 2006 the library of the Max Planck Institute for the History of Science acquired a copy of the first edition of Giovanni Battista Benedetti's3 Diversarum speculationum mathematicarum et physicarum liber.4 The book was purchased from an American bookseller who had acquired it at auction somewhere in Europe.5
Benedetti's book comprises six treatises: on arithmetical theorems,6 on perspective,7 on mechanics,8 on certain opinions of Aristotle9 (in particular concerning his theory of motion),10 on the fifth book of Euclid's11 Elements,12 and on physical and mathematical problems dealt with in letter form.13 The mathematical part concerns arithmetical principles, proving them geometrically; it also includes a discussion of perspective. The mechanical part contains a critique of sections of the Aristotelian Mechanical Problems14 and also investigates issues of hydrostatics.
While Benedetti's book is itself an important source for understanding the struggles of early modern engineer-scientists with the ancient heritage of mechanical knowledge due to Aristotle, Archimedes15 and others, this specific copy is of special value since it contains handwritten marginal notes by the leading expert on mechanics of the generation before Galileo,16 Guidobaldo del Monte,17 himself the author of the most influential Renaissance text on mechanics, the Mechanicorum liber.18
Part 3 of this book presents facsimile images of those chapters of Benedetti's work that contain the handwritten marginal notes by Guidobaldo del Monte. Similar marginal notes by Guidobaldo have been identified by Martin Frank in a copy of the first printed edition of a work by Jordanus de Nemore,19 the Liber de ponderibus20 edited by Petrus Apianus;21 these notes are reproduced in Part 2. With two exceptions the notes in Benedetti's book were written in the margins of the chapter on mechanics, covering 26 of the 428 pages of the whole book. The two remaining notes are added to two letters contained in a later part of the book. The second of these letters again deals with mechanics. This shows clearly that Guidobaldo was interested mainly in Benedetti's theory of mechanics. The contents of the notes indicate a strong criticism of Benedetti's theory, which is evidently related to objections raised by Guidobaldo also against Jordanus' work.
This criticism in Guidobaldo's notes concerns the central question of the equilibrium controversy: Does an equilibrated balance, if deflected into an oblique position of its beam, spontaneously return to the horizontal or does it remain in the deflected position? It will be shown, however, that this controversy only scratched the surface of a deeper-going conceptual crisis, indicated by the introduction – based on medieval sources – of a new, but ambiguous concept, the concept of positional heaviness. This crisis of the conceptual foundations of mechanics helped establish fundamental insights on which Galileo eventually built his theory of mechanics, as well as his theory of motion. More precisely, they concern the various controversial attempts to replace the ancient concepts of force and heaviness in the context of the causal interpretation of motion by modified concepts which were used to address the more complex technical experiences of the early modern period. We will show that the controversial opinions of Guidobaldo and Benedetti – as reflected in Guidobaldo's marginal notes on Benedetti's systematic treatment of the concepts of force and heaviness – concern core issues dealing with the problem of reorganizing the conceptual framework of ancient mechanics. In particular, Galileo's theory of motion along inclined planes, as well as many other of his characteristic themes, such as the motion of a pendulum, projectile motion, the motion of fall, and even his Copernicanism, were, as we shall argue, directly or indirectly related to this equilibrium controversy. In fact, Galileo's new science of motion would probably not have developed as it did without the insights he gained from Benedetti, or rather, from the conflictual encounter between Benedetti's and Guidobaldo's perspectives on mechanics.
The conceptual and historical background of the controversy will be extensively presented and analyzed in Part 1 of this volume. It will be shown that the equilibrium controversy was part of a long-term development which can only be understood against the background of the multi-layered architecture of human knowledge. In the case of mechanical knowledge, this architecture comprises first basic intuitive insights gained from everyday experience of the behavior of material bodies. Second, this knowledge architecture comprises the knowledge of practitioners who use, elaborate, and improve mechanical devices, thus extending the general intuitive mechanical knowledge by developing specific professional skills. Third, it comprises scholarly expertise represented by written manuals, innovative constructions, and scientific theories. Moreover, a profound analysis of the long-term development, from antiquity to the early modern period, of the basic concepts of mechanics involved in this controversy requires the exploration of the mechanisms of the synchronic and diachronic transmission of knowledge with regard to the different layers of its architecture. In the case of mechanics, an exploration of this kind reveals substantial differences between these layers regarding the conditions and the outcome of the knowledge transfer. While the basic intuitive mechanical knowledge depends on general environmental challenges and is thus widely available, practical knowledge requires transmission using historically created and reproduced mechanical instruments and devices. In turn, theoretical knowledge requires the transmission of external representations and the reflective reconstruction of their meaning by stable scholarly communities, which are thus often fragile due to contingent social conditions.
The analysis of the equilibrium controversy offers an opportunity to study the interaction of various components of mechanical knowledge, such as the Archimedean theory of the center of gravity and Aristotelian dynamics, and to investigate the consequences of the incomplete transmission of this knowledge through various transmission paths, from antiquity to the Arabic and Latin Middle Ages, and finally to the early modern period.22
1.3 Scientific controversies and challenging objects
Scientific controversies are ubiquitous; the field that is sometimes called rational mechanics is no exception. A famous example is the so-called vis viva controversy which arose toward the end of the seventeenth century and was concerned with the question of which agent produces certain mechanical effects and which physical magnitude is conserved in mechanical interactions. This debate eventually helped to arrive at the insight that there are conservation laws for both energy and momentum. But what exactly is a scientific controversy?23 At first glance, it may seem that a scientific controversy does not distinguish itself substantially from any other controversy, for instance, in politics or in religion. On closer inspection, however, the very existence of scientific controversies may seem a puzzling but perhaps irrelevant fact. If science essentially concerns the pursuit of truth, based on solid facts and guided by logical principles, then scientific controversies should arise only in unfortunate circumstances or when errors and misunderstandings occur. Ultimately, one if not all of the positions defended in the controversy would then be simply erroneous. In other words, scientific controversies may seem to reflect only the human aspect of science and its function as a social activity, undertaken by beings that do not always follow rational procedures. In this understanding, controversies in science are simply an accident of rationality, or even an indication that the alleged rationality of science does not exist at all and that science can be better understood without even making reference to it.
In view of the fact that controversies in science are so common and so closely related to its conceptual development, it seems, however, more plausible to assume that they are not simply a social or psychological phenomenon, but rather constitute an essential epistemic element of science and a medium of its historically developing rationality. A scientific controversy is understood here, using a definition proposed by Gideon Freudenthal, as a persistent antagonistic disagreement concerning a substantial scientific issue that cannot be resolved by the standard means available to science in the given period. In such a situation, the participants of the controversy attempt to defend their positions by showing that their understanding agrees with widely accepted explanations, that it allows them to explain certain challenging problems that may be objects of the controversy and to extend their interpretation to novel situations, hence broadening the empirical range of their approach. On the other hand, they attempt to show that their adversaries fail on some or all of these accounts. In reality, we may also encounter controversies that are not marked by an ongoing exchange between two antagonistic positions, but rather by a chain of criticisms among different protagonists or by a complex interaction involving different partners, issues and arguments. Nevertheless, the essential features EOAemphasized in the following apply to these cases as well.
Scientific controversies are often triggered by challenging objects.24 These are artifacts or other parts of the material culture that confront existing theoretical frameworks with explanatory tasks that cannot be accomplished with the available conceptual means, thus triggering their further development and ultimately their transformation. They typically embody other forms of knowledge, for instance, the practical knowledge of artisans to invent, produce, or make use of such objects. The development of the theoretical knowledge of mechanics in the early modern period can to a large extent be accounted for by the increasing attention scholars and engineer-scientists of the period paid to new objects of study which they investigated by means of the extant conceptual frameworks. These objects and phenomena had their origin predominantly in the rapidly developing technology of the day such as the pendulum and the flywheel used in machine technology or the projectile trajectory relevant to artillery. The practical experience gathered in the application of these objects in a technological context became one of the points of departure for related theoretical considerations. Before the onset of the experimental method, these objects were a key source of empirical knowledge which accounts for one aspect of their fundamental role in the conceptual reorganization of mechanical knowledge in the sixteenth and seventeenth centuries. Thus, Galileo's new science of motion, for instance, can be conceived as resulting from a struggle with the challenges represented by the pendulum and the motion of a projectile, both addressed on the basis of attempts to understand another challenging object, the inclined plane.
Challenging objects served as shared knowledge resources.25 In combination with the theoretical frameworks employed in their investigation, these objects largely determined the possible theoretical questions and answers. Focusing on such objects thus allows for an understanding of congruent theoretical developments – so characteristic for the period – which can hardly be accounted for by oral and textual transmission alone. Another stimulus for the development of the theoretical knowledge of mechanics is the fact that the theoretical accounts given for these challenging objects often sought to mirror and account for the complex relations of these objects in their technological context to other mechanical objects and phenomena of interest, and in particular to the so-called simple machines. In many cases this led to the integration of previously disparate mechanical knowledge. This evidently represents an important mechanism for the unification of mechanical knowledge. A key example that will be discussed below is Galileo's identification of the inclined plane with a bent lever and his attempt to explain the former in terms of the latter.
Scientific controversies are possible because they refer to the shared knowledge of its participants and they presuppose a common structuring of this knowledge by shared conceptual systems. They arise because the discussants adopt different interpretations of the same framework and draw different conclusions from it. For example, it may turn out that the same phenomenon can be conceived in two alternative manners. This may happen even within a single conceptual system, but is all the more likely as the relevant shared knowledge typically involves diverse conceptual systems or alternative options for choosing foundational concepts that may then serve as starting points for conceptualizing the given phenomenon. In any case, in the course of the exploration of the shared knowledge, partial differences of meaning may arise. The fact that these differences are only partial allows a meaningful exchange over the course of the controversy, while the very existence of these differences makes the controversy itself unavoidable.
Typically, scientific controversies are not resolved by victory, but rather by a further development and subsequent transformation into a new conceptual framework in which the original question often changes or even loses its meaning. Thus, the original issue of the vis viva controversy concerned two alternative proposals for the causal agent of certain effects, as well as the question of what physical magnitude is conserved. Eventually this alternative gave way to the understanding that there are actually two distinct magnitudes, momentum and energy, which are effective and conserved in physical interactions. But even when no party prevails, one of the opposing positions may have a greater impact on the emergence of a novel conceptual system. In any case, both antagonistic positions can be recognized, in hindsight, as alternative interpretations of the same underlying conceptual basis. This is precisely the hallmark of a more developed conceptual framework, that it allows a reconstruction of the previous positions, while it cannot be expressed itself in terms of the previous framework.
From this epistemological perspective, a number of typical features may be recognized that characterize a scientific controversy, such as the multiplication of examples in one's favor, attempts to reconstruct the adversary's position from one's own perspective, but also the unavoidable occurrence of misunderstandings, and a shift toward a more reflective stance, following the lineage of the premises of the argument defended. All of these moves effectively constitute a further exploration of the limits of the conceptual framework available to the historical actors. This conceptual framework is in fact never given from the outset in its entirety, that is, in all of its potential conclusions and applications, but actually only unfolds with the unfolding of the real scientific practice in which it is embedded. Conceptual development in this sense is hence the development of the shared knowledge of the community of practitioners, and their controversies are one essential form in which this development takes place. Its effectiveness may therefore depend on the specific historical conditions, be they material, social, or intellectual, favoring or impeding the possibility of controversies. As a result, some controversies may be resolved, in the sense outlined above, in a very short time, while others, such as the one treated here, may extend over centuries.
1.4 The physical background of the equilibrium controversy
The first balances were constructed in the grand early civilizations of antiquity, in Babylonia, in Egypt, and in China. They are attested since about the third millennium BCE. The introduction of balances was associated with the establishment of a quantified concept of weight. The balance also attained a symbolic significance from very early on, but its functioning did not become the subject of any written accounts before Greek antiquity. In fourth-century Greece, balances with unequal arms were invented, an invention which opened up the possibility of equilibrating different weights on one side of a balance with a single weight in different positions on the other side. This invention eventually gave rise to the formulation of the law of the lever as we find it in the works of Aristotle, Archimedes, Heron, and others. In modern terms, the law of the lever can be expressed as the equality of the product of weight and lever arm at each side of a balance in equilibrium. The invention of the balance with unequal arms also gave rise to the insight that the effect of a weight may depend on its position, the central subject of this book.
Numerous studies have been dedicated to the balance in practically all times and cultures, in particular, in the Arabic and Latin Middle Ages, as well as in the early modern period. The understanding of the balance became, more than that of any other instrument, the paradigm of mechanical knowledge, the core of a science of weights. For more than two millennia the balance served as a generator or touch stone for physical concepts, from the law of the lever to the principle of the conservation of energy. How could this happen? Here we deal not with the fascinating history of the balance as a key model of physical science, but focus rather on a specific aspect of this history which is related to the positional effect of a weight placed on a balance.
A balance with equal arms and equal weights is in equilibrium. We normally imagine such a balance in its default position, its arms aligned along the horizontal, perhaps with the two equal weights placed in two scale pans, appended to the beam of the balance at equal distances from its suspension point. But what happens when the balance is deflected from this horizontal position? The following study will show that historically the default expectation was – and is probably the case even today – that it returns to this position, which indeed happens for most balances in practical use. If we are taught by a modern physicist that this question can be answered, due to classical physics, within a theory of mechanics that is based on a network of causes involving concepts such as center of gravity, torque, bent lever, the position of the fulcrum, and friction, we are, of course, willing to concede that the equilibrated balance may not be as simple a physical device as it initially appeared. We may also learn that an ideal balance does not actually return to the horizontal position, but that it will rather stay in whatever position it is brought, thus illustrating the concept of an indifferent equilibrium.
Apparently, more sophisticated knowledge is required to answer even the seemingly simple question of whether a deflected balance will return to its original position. But from where did this sophisticated knowledge come? Modern physical theories such as theoretical mechanics no longer carry with them easily recognizable traces of the origin of their concepts. Physicists tend to assume that the correct answer to a problem such as that of the deflected balance must have ultimately emerged from careful experiments, the results of which were integrated into a proper theoretical framework. Without such a framework, even the most sophisticated experimental explorations will in fact yield nothing but an accumulation of data on single cases without a basis for generalization.
But how could such a theoretical framework emerge when observations concerning even the most elementary case of a deflected balance remained inconclusive, as they apparently did for more than two millennia? The question of whether or not an equilibrated balance would return to its horizontal default position or remain indifferent in whatever position it is brought was not in fact settled before the early modern period when it became the explicit subject of a controversy between Guidobaldo del Monte and other protagonists of preclassical mechanics,26 in particular Benedetti.
There is, of course, the possibility that the knowledge necessary to decide this equilibrium controversy developed from sources other than the study of balances, as it certainly did to some extent. Without confronting other challenging objects such as the so-called simple machines, the lever, the wheel and axle, the pulley, the inclined plane, the wedge, and the screw, theoretical mechanics would not have evolved as it did. From its beginning in Greek antiquity, the aim of mechanics was to explain the communality of a set of mechanical devices and, in particular, of how they made it possible to achieve a large effect with a small force. Nevertheless, in much of the history of mechanics up to the early modern period, it was the balance that kept its paradigmatic role in forming and exploring basic concepts such as equilibrium and the positional effect of a weight. A study of the history of the equilibrium controversy, culminating in the confrontation between Guidobaldo and Benedetti, therefore also offers the opportunity to analyze this pivotal role of the balance more closely.
An ideal balance with equal arms and equal weights, that is, a balance with a weightless beam suspended from its center of mass in a homogeneous gravitational field, will indeed be in an indifferent equilibrium. When it is brought into any position compatible with its mechanical constraints, it will stay there. The weights at the end of the beam of the balance exert forces on the beam. Together with the arms at each side of the beam these forces form a torque, also called moment or moment of force, causing a tendency to rotate the balance. In the case of the ideal balance described above the torques are equal, which explains the equilibrium of the balance from a modern point of view.
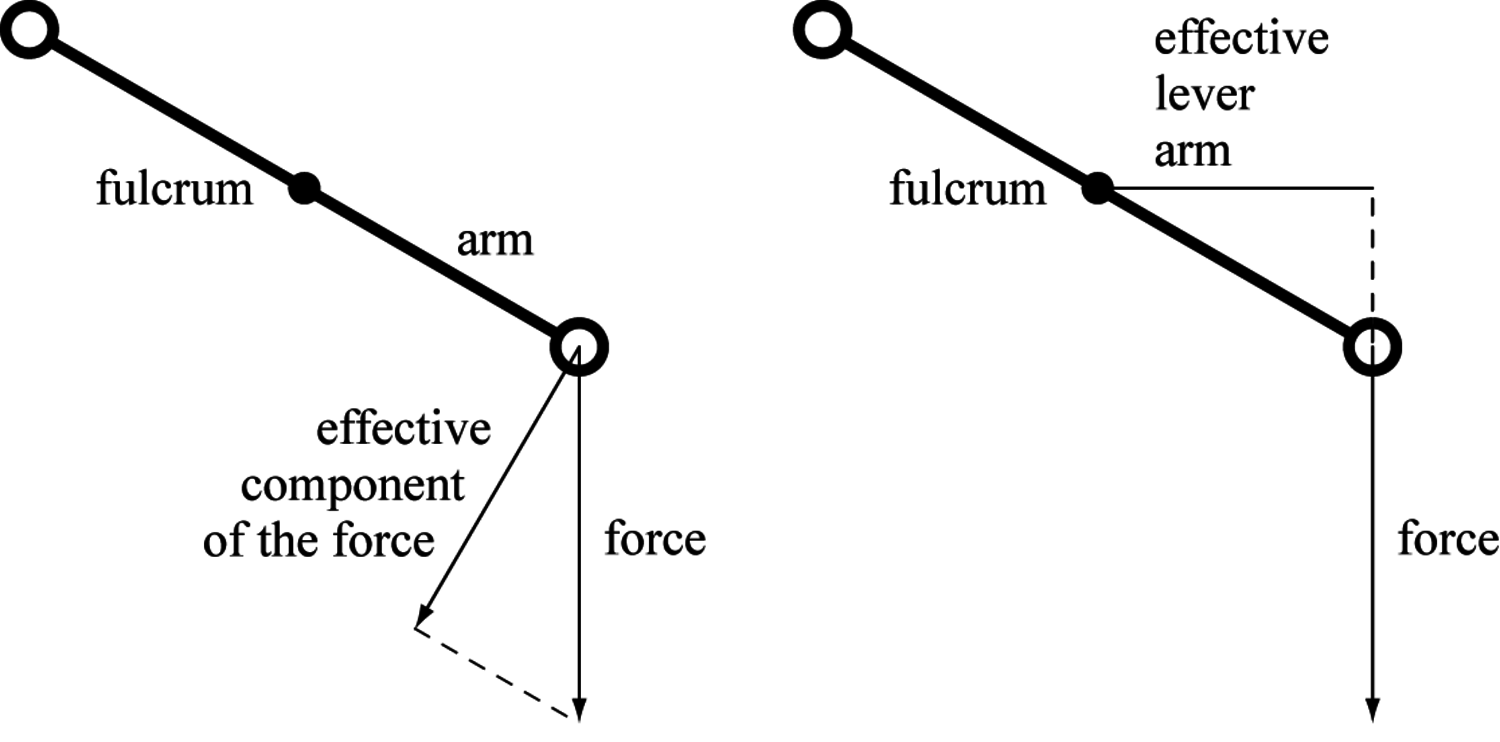
Fig. 1.2: The torque of a weight attached to one side of a balance is given by the product of the arm and the effective component of the force acting perpendicularly to it, or, which is equivalent, by the product of the force and its effective lever arm, which is the component of the real lever arm perpendicular to the force.
The torque is given, more specifically, by the product of the arm and the effective component of the force acting perpendicularly to it. Alternatively, the torque can be expressed as the product of the force and its effective lever arm, which is the component of the real lever arm perpendicular to the force (see figure 1.2).27 While the equivalence of both definitions is immediately clear if the algebraic notation of modern physics is used, it needs a more sophisticated argument to prove it purely geometrically using the mathematics of the time of preclassical mechanics.
If the balance is in a horizontal position, the torque at one side is simply the product of the weight and the balance arm at that side. If the balance is in an oblique position, the torque can be found by projecting the arm of the balance on the horizontal and multiplying the length of this projection, that is, the effective lever arm, with the weight. In modern understanding, the torque is actually a vector product, a concept not established before the nineteenth century. The requirement that the torques are equal for a balance in equilibrium can be conceived of as a generalization of the law of the lever. This generalization is applicable not only to balances with unequal arms, but also to balances with arms that are not aligned or, in other words, to the so-called bent lever. If one arm of a balance is aligned with the horizontal, while the other arms is bent at an angle, it is again the projection of the bent arm on the horizontal that acts as the effective lever arm. This way of determining the effective lever arm by a projection on the horizontal was EOAemphasized – as we will see below – by Benedetti and opposed by Guidobaldo.
The concept of torque is not the only modern concept to explain the equilibrium of a balance or the behavior of a bent lever. They can also be analyzed with the help of the concept of mechanical work. This concept is more generally applicable to physical systems than the concept of torque and, in a sense, even more intricate as a glance at its definition in classical physics makes clear. In general, the work performed by a force on a body along a trajectory is given by the line integral of the scalar tangential component of the force along the trajectory. Generally, the force is changing along the path, as it does in the case of a balance arm moving from the horizontal into an oblique position. The line integral of the changing force is given by the infinite sum of infinitely small displacements on the trajectory multiplied with the forces acting in these infinitesimal displacements. The changing force may have arbitrary directions, but according to the definition of mechanical work only the component of the force acting along the path of the displacement or, which is the same, the component of the path traversed along the direction of the force has to be taken into account. In modern terminology, this is the time integral of the scalar product of the force vector and the velocity vector along the trajectory, in contrast to the vector product of the lever arm and the force relevant to the consideration of the torque. Thus, the concept of work is even more demanding than the concept of torque because it involves the infinitesimal calculus so that the historical actors considered here, living before its introduction in the age of Newton28 and Leibniz,29 had no chance to fully master this concept.
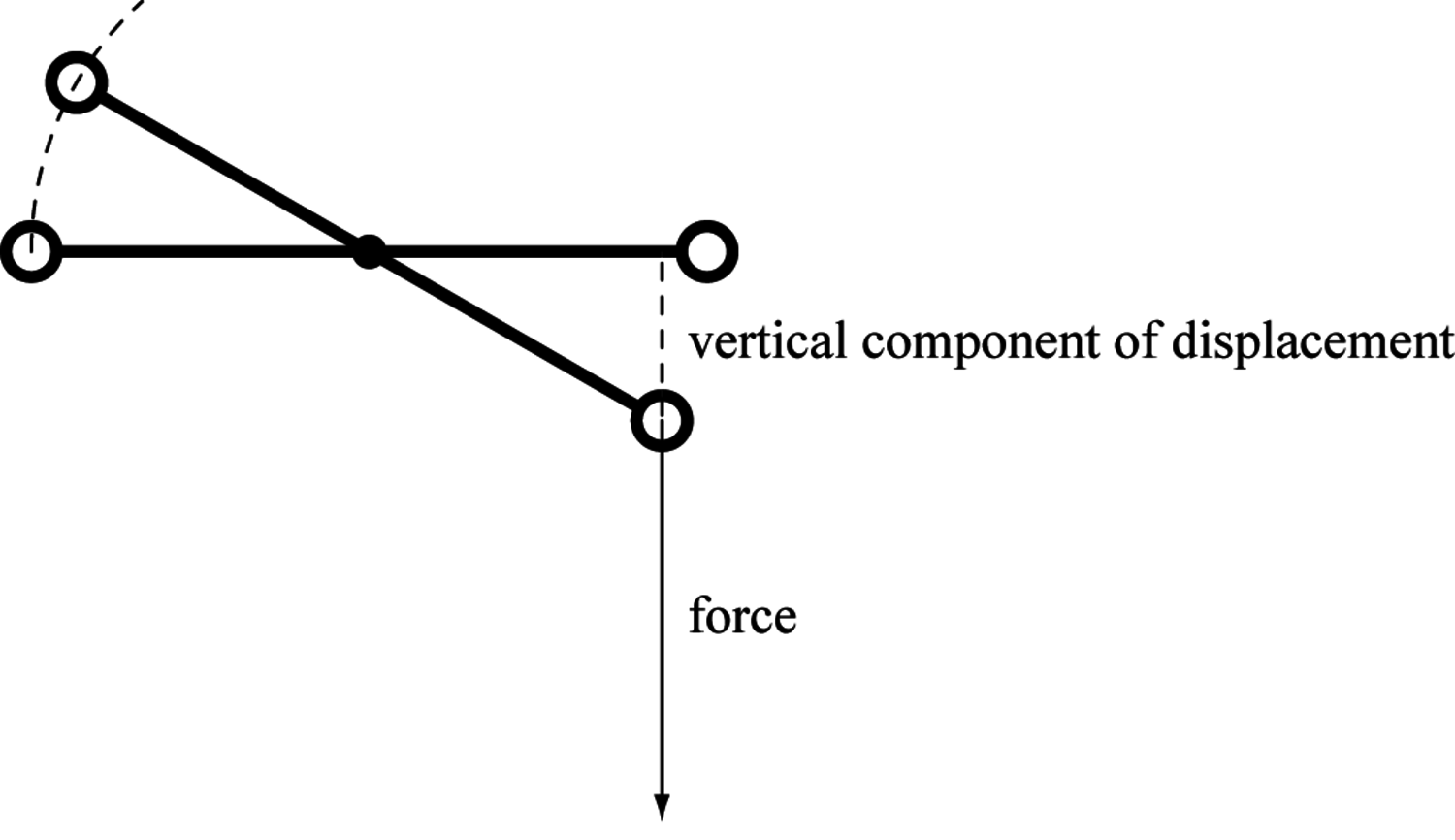
Fig. 1.3: In the specific case of a balance in a homogeneous field of gravitation the mechanical work of a weight attached to one of its arms is given by the product of the constant gravitational force and the vertical component of its displacement.
Only in the most simple cases can mechanical work be thought of as the product of a force and the distance over which it acts. In particular, the work performed by the force of gravity does not depend on the path taken by a body. The vertical component of the force of gravity can be considered as practically constant and the varying horizontal component requires no force and thus has no influence on the mechanical work of the motion along the trajectory. Therefore, the work can be determined in this specific case by just considering the vertical distance traversed, for instance, by a weight on a balance beam (see figure 1.3). The equilibrium of a mechanical constellation can then be characterized by the demand that the total work performed by a displacement of the entire constellation in agreement with the mechanical constraints is zero. Now the work performed by one weight is simply given by the product of the vertical component of its displacement by the force of weight. In the case of a balance with unequal arms, the vertical components of the displacements of the two weights are proportional to the lengths of the arms of the balance. Hence the total work performed by a displacement, for instance, by bringing the balance from the horizontal into some oblique position, is zero if the products of weight and length of the arm are equal on both sides. Then the work performed by lifting the weight on one side of the balance will be equal to the work gained by lowering the weight on the other side of the balance. In this way, the inverse proportionality of weights and arms follows, as stated by the law of the lever.
This way of determining mechanical equilibrium can be also illustrated by the case of an inclined plane: Let a weight be placed on the inclined plane and connected via a weightless rope through a wheel at the top to another weight hanging down on the other side, moveable along the vertical such that when the weight along the plane is moved upwards, the other weight is moving perpendicularly downward. In equilibrium, the total work performed by the system must be zero. For the weight moving along the vertical, the work performed is simply the product of the weight and the total displacement which happens to be along the vertical. For the weight moving along the inclined plane, the work performed is the product of the weight with the vertical component of the displacement along the plane. Given the connection through the rope, the total displacement along the plane must be the same as the total displacement of the weight moving along the vertical. In the case of equilibrium, the product of the weight along the vertical with the total displacement must be the same as the product of the vertical component of the displacement along the plane with the weight on the plane. But this vertical component is to the total displacement as is the height of the plane to its length. It hence follows that the product of the weight in the vertical and the length of the plane must be the same as the product of the weight on the plane and the height of the plane, or in other words, the weight along the vertical is to the weight on the plane as is the length of the plane to its height. This is the famous law of the inclined plane, as it was first stated by Jordanus. Remarkably, his proof also works with the consideration of vertical displacements which is why it has often been associated with the principle of work (see figure 3.13).
Such associations are in fact merely the product of anachronistic projections. They suppose an essentially teleological development of the history of scientific concepts in which earlier concepts are merely embryonic forms of the mature ones. A closer look at the equilibrium controversy makes it evident that such a perspective is of little help in understanding the nature of the historical process. None of the protagonists of this controversy strove for the introduction of novel physical concepts such as torque or work. They were actually merely concerned with a better understanding of the concept of weight and of the way a weight acts under given mechanical circumstances. They also did not attempt to differentiate between those physical aspects captured by the modern concepts of torque and work. While the modern concept of work indeed covers all mechanical devices, the concept of torque only applies to cases in which a lever arm is involved. Also, while the torque refers to the way a force acts at a particular point in space and time, the concept of work, being represented by an integral, refers to the action of a force along a certain path.
The participants in the controversy attempted instead to find a universal way in which the effectiveness of a weight varying with the mechanical circumstances could be described so as to be applicable to all mechanical devices. The concept of positional heaviness, introduced by Jordanus in the thirteenth century, represents such an attempt. One key aspect of the controversy was, as we shall extensively discuss in the following, the question of whether positional heaviness is to be measured by the projection of the lever arm on the horizontal (as the torque) or by the vertical component of a displacement of the weight on the lever arm (as the work). From a modern perspective this alternative makes little sense as it refers, as we have seen, to two distinct physical concepts that cannot always be applied to the same situations. How hopeless the attempt was to capture both aspects by a single, modified concept of weight becomes clear if one considers that the modern concept of torque refers to a point, while the concept of work refers to a displacement. Nevertheless, the equilibrium controversy contributed significantly to preparing the ground for the emergence of the later conceptual distinctions of classical physics, in particular, with the ambiguities and paradoxes that surfaced as it unfolded.
One of these paradoxes was the perplexing difficulty in establishing a stable answer to the simple question of whether an ideal balance deflected from its horizontal default position would return to it or not. By referring, as we did above, to an ideal balance we have actually introduced tacit premises, in particular, that the lines of force are parallel and that the gravitational force remains the same even when the balance is displaced from its default position. In short, we have neglected the cosmological context of the balance, the fact that the weights carried by its beam tend to fall not along parallel lines, but along lines meeting at the center of the earth and that the force of gravitational attraction may vary with distance. Clearly, the effects introduced when these circumstances are taken into account must be vanishingly small and practically irrelevant. They can, however, not be as easily dismissed as for instance the role of friction as they directly pertain to the understanding of the very concept of weight at the center of the analysis of the balance. Moreover, the cosmological context of a physical problem like that of the equilibrium of the balance was particularly important to the debates of the early modern period where such problems were inevitably related to larger issues of the physical world view. In fact, Aristotelian natural philosophy was the dominant conception of nature at the universities and, beginning with the Council of Trent, had been embraced as the official world view of the Church. It is therefore not surprising that, in this period, the cosmological dimension played a critical role for the equilibrium controversy.
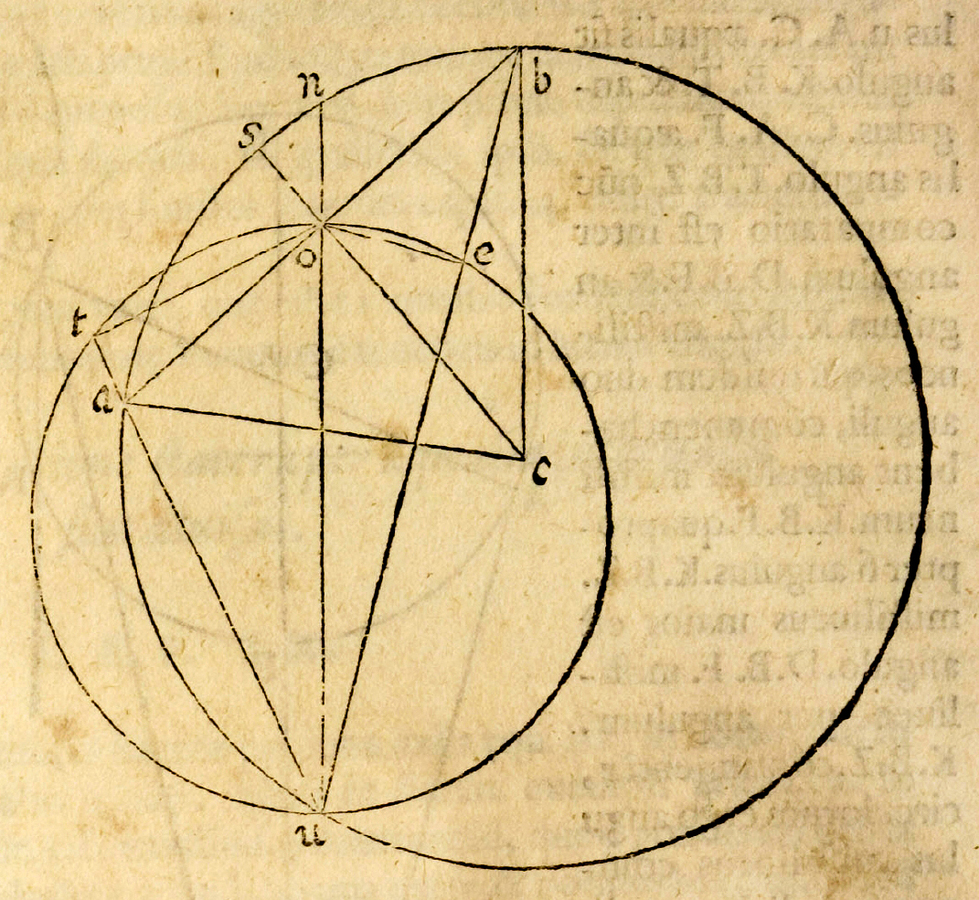
Fig. 1.4: A diagram from Benedetti's book representing a balance AB supported at O in a cosmological context where U is the center of the earth. The weights in A and B have a tendency to fall toward U. The lines OT and OE drawn from the point of suspension are perpendicular to the lines AU and BU connecting the weights with the center of the earth.
It is not difficult to reconsider the question of the behavior of an equilibrated balance in a context in which the lines of force connect the weights to the center of the earth and in which the forces themselves may vary with the distance from that center (see figure 1.4). How does such a cosmological balance behave from the perspective of later classical physics? The torque of one of the weights placed at the end of the beam is given by the projection of the respective balance arm onto a line that now plays the role that the horizontal had played in the ordinary balance. This line is obtained by drawing, from the point of suspension, a perpendicular onto the line connecting the weight with the center of the earth. Similarly, the torque of the weight on the other side of the balance can again be determined by constructing a perpendicular onto the line connecting this weight with the center of the earth. It now turns out that the ratio between the two lines measuring the torques at the two sides of the balance is the inverse of the ratio of the two lines connecting the weights to the center of the earth, if it is assumed that the gravitational force does not change with distance. As a consequence, the torque on the side of the balance which has descended is larger than the torque on the side which has been raised so that the cosmological balance would neither stay indifferent nor return to the default position, but rather align itself along the vertical. This was also the conclusion that Benedetti reached and to which Guidobaldo violently objected. If it is furthermore assumed that the gravitational force does vary with distance, becoming weaker as the distance increases (as in reality), the effect that the balance turns into the vertical is even strengthened. Under the given circumstances, the only way to obtain an indifferent equilibrium is to assume that the gravitational attraction behaves the other way around, becoming stronger as the distance increases, as if it were a rubber band by which bodies are confined to their center of attraction.
Guidobaldo, the most influential writer on mechanics of the sixteenth century, was proud to have reconciled the Archimedean theory of equilibrium, based on the concept of center of gravity, with the Aristotelian understanding of weight as tending to the center of the world. This reconciliation was embodied by what was evidently, in his view, the greatest discovery he had made: the insight that both an ideal balance and also what we have called a cosmological balance remain in indifferent equilibrium. His adversary Benedetti claimed that, while such an indifferent equilibrium holds under terrestrial circumstances, it is impossible for a cosmological balance. He thus challenged Guidobaldo's grand synthesis. While Benedetti's conclusion is in accordance with later classical physics, the controversy could hardly be settled definitively with the arguments available at the time. It was the equilibrium controversy more than its resolution that spurred the further development of physics.30
1.5 Editorial remarks
Latin and Italian texts are transcribed using orthographic normalization, that is, punctuation, accents, and capital letters have been revised according to standard Latin and Italian. As a rule, abbreviations and symbols have been expanded or resolved. Arabic names are romanized. Translations are adapted from standard references, when available, and modified whenever necessary. All further translations, unless otherwise indicated, are by the authors.31
Some of Guidobaldo's marginal notes to Benedetti's text were deleted and are now unreadable. Some notes have been cut off by a bookbinder. Such passages have been amended as far as possible.
The considerable number of deleted passages raised the question of whether it would be possible to read the text underneath the deletions by applying special analytical methods and also whether the deletions have been performed by the same author who wrote the notes. In order to answer these questions the composition of the ink has been examined by means of an X-ray fluorescence analysis (XRF), performed at the Federal Institute for Materials Research and Testing in Berlin.32 The result of the preliminary analysis is that the deletions were made in the same ink and hence most probably by Guidobaldo himself and that the text underneath cannot be rendered legible by a non-destructive analysis.
The copy of DelMonte 1577, reproduced in the first volume of the present series, Renn and Damerow 2010, is itself a testimony to the equilibrium controversy. Passages relevant to the controversy have been underlined using an iron gall ink from the period but distinct from that used by Guidobaldo himself in his marginal notes to Benedetti's work. The composition of the ink has also been analyzed by means of an X-ray fluorescence analysis, performed at the Federal Institute for Materials Research and Testing in Berlin (see figure 1.5).

Fig. 1.5: X-ray fluorescence analysis of the ink used in underlinings found in a copy of Guidobaldo's mechanics. The underlinings were written with an iron gall ink from the period. They concentrate on the foundational aspects of Guidobaldo's approach, his comments on Aristotle, and the critique of his adversaries.
Footnotes
For historical discussion, see Janssen 1995.
Giovanni Battista Benedetti, 1530–1590.
We would like to warmly thank Enrico Giusti for bringing our attention to the possibility of purchasing this work for the library of the Max Planck Institute for the History of Science in Berlin and Urs Schoepflin, its director, for pursuing the acquisition so efficiently.
Benedetti 1585, 141–167, pages 322–374 in the present edition.
Aristotle, 384–322 BCE.
Euclid of Alexandria, fl. ca. 300 BCE.
Benedetti 1585, 204–426, partly reproduced on pages 376–416 in the present edition.
Aristotle 1980. The attribution of this work to Aristotle is controversial. While in the early modern period it was widely considered to be an original work of Aristotle, later philologists have questioned his authorship, ascribing it to one of his immediate followers; see Krafft 1970 and Rose and Drake 1971, 72. For more extensive discussions, see section 3.4.1.
Archimedes, around 287–212 BCE.
Galileo Galilei, 1564–1642.
Guidobaldo del Monte, 1545–1607; often formerly referred to as Guido Ubaldo.
DelMonte 1577, see the first volume of the present series Renn and Damerow 2010. The volume contains a complete facsimile reproduction of Guidobaldo's publication. Guidobaldo's authorship of the marginal notes is indubitably evidenced not only by the style of handwriting, but also by some references in the notes to his own publications. The indications in the notes, which allow the identification of Guidobaldo as their author, were listed in the description of the book in the auction catalog (Martayan Lan Catalogue 38). This description is based on work by Anthony Grafton, who also provided a transcription of some key passages.
Jordanus de Nemore (also Jordanus Nemorarius), fl. early thirteenth century.
Petrus Apianus, 1495–1552.
The timeline in chapter 9 provides an overview of this long-term development.
Here we closely follow the arguments and the definition of a scientific controversy suggested by Gideon Freudenthal in the context of a jointly developed epistemological framework, see Nemore 1533. His contributions also offer relevant examples from the history of mechanics as well as comments on the literature about scientific controversies; for the jointly developed epistemological framework, see Damerow et.al. 2004.
The idea to approach the history of early modern mechanics from the perspective of its challenging objects was first launched in Renn 2001. It has since been widely taken up, see in particular Büttner et.al. 2004, Bertoloni Meli 2006, Büttner 2008, Büttner 2009 and Valleriani 2010. The notion as it is here presented has been jointly formulated with Jochen Büttner.
For the concept of shared knowledge, see Renn 2001 and Büttner et.al. 2004.
For the concept of preclassical mechanics, see Damerow et.al. 2004; see also Renn et.al. 2001, Büttner et.al. 2004; Valleriani 2010; Damerow and Renn 2010; Büttner 2008; furthermore see the broad discussion in Bertoloni Meli 2006.
Isaac Newton, 1642–1726.
Gottfried Wilhelm Leibniz, 1646–1716.
The equilibrium controversy was not settled during the period under consideration here. Also, we have not attempted to be exhaustive in dealing with all pertinent contributions. For glimpses of other aspects of the controversy and its historical sequel in the recent literature, see Roux 2004, 36–39 and Bertoloni Meli 2006, 31–32. A particularly interesting case is the treatise on mechanics from 1597 by Colantonio Stigliola, 1546–1623, see Gatto 2006. For a discussion of the role of the bent lever as a challenging object in the relativity revolution, see Janssen 1995.
Translations of Benedetti, Guidobaldo, and Tartaglia, for example, are taken from Drake and Drabkin 1969, sometimes with slight modifications.
See the appendix.
