In general relativity there is no obvious reason why masses shouldn't be negative, so we will investigate this concept. We can get three definitions of mass: inertial mass, passive gravitational mass on which the field acts and active gravitational mass which is the source of the field. In Newtonian theory, due to action and reaction, passive and active gravitational masses must be the same. The fact that passive and inertial masses are the same is the consequence of experiments. In general relativity, passive and inertial masses are the same due to the principle of equivalence. The first place where active gravitational mass occurs is the
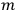 in the Schwarzschild solution. There is no action and reaction principle, and we know that active and passive masses may not be equal. In Newtonian theory, the most obvious notion of a negative mass is similar to charge; like masses attract and unlike repel. In general relativity, a negative mass repels all masses, a positive attracts all. If we have a system with one mass of each type, the system will uniformly accelerate. I have constructed an exact solution of the field equations which shows these properties. The solution fills only one-fourth of space-time. I have found a method of continuing the solution into the other regions.
in the Schwarzschild solution. There is no action and reaction principle, and we know that active and passive masses may not be equal. In Newtonian theory, the most obvious notion of a negative mass is similar to charge; like masses attract and unlike repel. In general relativity, a negative mass repels all masses, a positive attracts all. If we have a system with one mass of each type, the system will uniformly accelerate. I have constructed an exact solution of the field equations which shows these properties. The solution fills only one-fourth of space-time. I have found a method of continuing the solution into the other regions.
BERGMANN: I think one can show that within the general theory, it is not possible to have the active and passive masses different.
BONDI: This is a question of conservation of momentum, which means integrals over extended regions of space. But what do you say about the Schwarzschild interior solution where the
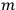 is certainly not just the integral of the
is certainly not just the integral of the
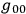 ?
?
GOLD: What happens if one attaches a negative and positive mass pair to the rim of a wheel? This is incompatible with general relativity, for the device gets more massive.
BONDI: The purpose of this is to show that negative mass is incompatible, but I haven't got there yet.
PIRANI: I want to reply about active and passive mass. One can show simply that they are different and that the density of one is got by taking the density of the other and subtracting the principal stresses.
A Dynamic Instability of Expanding Universes R. Mjolsness
Small deviations of the metric from exact sphericity are considered in order to investigate the stability of the standard Friedman solution. An oscillating cosmological model is used with positive curvature and zero cosmological constant. In order to solve the problem exactly, a relation between the pressure and the density is needed. Two cases are considered for which this relation is known; the dust-filled and the radiation-filled universe. This problem is similar to one done by Lifschitz in 1946. He wished to discover whether one can account for the formation of nebulae in an expanding universe of negative curvature. He found that the perturbations do not grow sufficiently rapidly. Here, the question is reopened, for the perturbations do grow sufficiently rapidly. Deviations of the metric from spherical symmetry are expanded in terms of tensors formed from hyperspherical harmonics. Two of the four types of tensors formed give no contribution to a change in the density, but two of them do. These two result in two coupled ordinary differential equations. The case of the dust-filled universe is completely solvable and unstable. Work on the radiation-filled case has been started. Here it appears that there is a solution in which the perturbations grow. There is a close analogy with the problem of an oscillating underwater bubble which is well known to show Rayleigh-Taylor instability against small departures from a spherical form.
BONDI: Have you tried this for the Newtonian cosmological models of Milne and McCrae?
BONDI: They have an extremely close analogy; on the cosmological and galactic scale we get the same equations. I have played about with that, and I think that you always get that while the relative density fluctuations increases, the density goes down.
WEBER: In the topological models of Wheeler, one forms charges out of fields. The question arises how one can measure fields without charges. I will outline one method. If a neutral body is constructed out of fields and placed in an external uniform field, the body will become polarized and appear to have a dipole moment. If two such neutral bodies are placed in a field, one can determine the existence of an external field from their motion. In addition, the fact that a field is capable of polarizing a neutral body implies that a neutral body should repel a charged body.
This may have some cosmological significance, but the forces are very small.
SCIAMA: Instead of studying all of the complexities that exist in the symmetric theory of gravitation, I want to propose the possibility that the theory of the pure gravitational field should be based on a non-symmetric potential if the sources have spin. When one tries to define spinors in such a scheme, certain definite statements about elementary particles may be made, which can be checked within a year or two. The original motivation for introducing a non-symmetric potential is heuristic. From special relativistic field theory, we know that the energy momentum tensor is non-symmetric if the system has spin. Belinfante has shown how this tensor can be symmetrized. This procedure constructs a complicated energy momentum tensor whose moment contains the spin; but the spin is not fundamentally a moment, as orbital angular momentum is.
As a purely heuristic argument, it might be less artificial to keep the energy momentum tensor non-symmetric, so that it is apparent that the system possesses spin. In that case, one is forced to construct a theory of gravitation with a non-symmetric potential. However, we make an exception of fields with zero rest mass, for in this case we cannot make a distinction between spin and orbital angular momentum. We construct a theory whose mathematics is similar to Einstein-Schrödinger type theories, but has nothing to do with the electromagnetic field. We find that the orbital angular moment in the special relativistic limit is the moment of the canonical stress energy tensor. The quantity
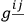 plays the same role in the equations of motion of a scalar test particle as
plays the same role in the equations of motion of a scalar test particle as
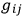 in the symmetric theory. To introduce spinors in the non-symmetric theory, we use a Hermitian metric with symmetric real part and non-symmetric imaginary part. This allows us to introduce complex vierbeine, so we can perform unitary transformations rather than rotations and this leads to a Hermitian requirement for the energy momentum tensor. To get something analogous to spinors, we must discuss quantities that transform irreducibly with respect to the unitary group. There are two main differences between this group and the Lorentz group. First, the Lorentz group is composed of four disconnected parts, while the unitary group envelops all continuously. This suggests that parity must be conserved in such a scheme. These representations are complex, and thus describe charged particles; strictly neutral particles must be described by real wave functions and thus are subject only to the Lorentz subgroup and will have symmetric energy momentum tensors. Neutral particles may not conserve parity. Also, neutral particles must have zero spin, zero rest mass, or both. The second difference relates to topological properties; the topological properties of the unitary group are more complicated, and this allows one more freedom in constructing representations. A phase transformation is included under the unitary group. If one has only one field, the phase transformation cannot be determined; but if several fields interact, this leads to selection rules. The question now is can we arrange these rules to forbid certain interactions which are known not to occur in nature, which are consistent with the present selection rules. This work is not yet complete; but one can presumably find rules which will prevent heavy particles from decaying into light particles, and thus understand the conservation of heavy particle number.
in the symmetric theory. To introduce spinors in the non-symmetric theory, we use a Hermitian metric with symmetric real part and non-symmetric imaginary part. This allows us to introduce complex vierbeine, so we can perform unitary transformations rather than rotations and this leads to a Hermitian requirement for the energy momentum tensor. To get something analogous to spinors, we must discuss quantities that transform irreducibly with respect to the unitary group. There are two main differences between this group and the Lorentz group. First, the Lorentz group is composed of four disconnected parts, while the unitary group envelops all continuously. This suggests that parity must be conserved in such a scheme. These representations are complex, and thus describe charged particles; strictly neutral particles must be described by real wave functions and thus are subject only to the Lorentz subgroup and will have symmetric energy momentum tensors. Neutral particles may not conserve parity. Also, neutral particles must have zero spin, zero rest mass, or both. The second difference relates to topological properties; the topological properties of the unitary group are more complicated, and this allows one more freedom in constructing representations. A phase transformation is included under the unitary group. If one has only one field, the phase transformation cannot be determined; but if several fields interact, this leads to selection rules. The question now is can we arrange these rules to forbid certain interactions which are known not to occur in nature, which are consistent with the present selection rules. This work is not yet complete; but one can presumably find rules which will prevent heavy particles from decaying into light particles, and thus understand the conservation of heavy particle number.
KURSUNOGLU: In this theory with a complex representation of field variables, isn't the velocity of light greater than its normal value as it is with Einstein's
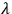 invariance?
invariance?
SCIAMA: I presume that the motion of light will be given by the same quantity that governs the equations of motion.
BERGMANN: This is a different theory, you don't have
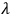 invariance.
invariance.
A discussion of the recent discoveries regarding parity followed. Professor ROSENFELD spoke of the contents of a recent note from Landau in which he suggested that in weak interactions, the coupling is not invariant for parity, or charge conjugation, but for the product of the two. By introducing this combined parity, one is left with invariant couplings; one can't have one of the transformations without the other.
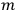 in the
in the 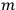 is certainly not just the integral of the
is certainly not just the integral of the
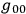 ?
?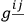 plays the same role in the equations of motion of a scalar test particle as
plays the same role in the equations of motion of a scalar test particle as
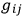 in the symmetric theory. To introduce spinors
in the symmetric theory. To introduce spinors 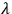 invariance?
invariance?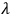 invariance.
invariance.